/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 1465656

Dodaj do ulubionych
Dodaj do rozwiązanych

Na loterii jest 20 losów, wśród których jeden los wygrywa 600 zł, pięć losów wygrywa po 200 zł i sześć losów wygrywa po 150 zł. Pozostałe losy są przegrywające. Jakie jest prawdopodobieństwo tego, że kupując jako pierwsi cztery razy po jednym losie wygramy dokładnie 600 zł?

Rozwiązanie

Losów przegrywających jest

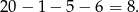
2 0− 1− 5 − 6 = 8.

Cztery losy spośród 20 możemy wybrać na

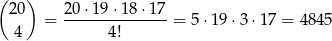
( 20) 20 ⋅19 ⋅18 ⋅17 = -------------- = 5⋅19 ⋅3 ⋅17 = 4 845 4 4!

sposobów.

Zdarzeń sprzyjających z losem wygrywającym 600 zł jest

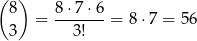
( ) 8 = 8-⋅7-⋅6 = 8 ⋅7 = 5 6 3 3!

(do losu wygrywającego dobieramy 3 przegrywające). Zdarzeń sprzyjających z trzema losami po 200 zł jest

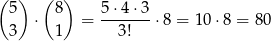
( ) ( ) 5 8 5-⋅4-⋅3 3 ⋅ 1 = 3! ⋅8 = 10 ⋅8 = 8 0

(wybieramy trzy losy wygrywające 200 zł i jeden los przegrywający). Wreszcie zdarzeń z czterema losami po 150 zł jest

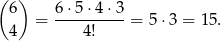
(6) 6⋅5 ⋅4 ⋅3 = ----------= 5 ⋅3 = 1 5. 4 4 !

Interesujące nas prawdopodobieństwo jest więc równe

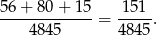
56 + 8 0+ 15 151 ------------- = -----. 48 45 4 845

 
Odpowiedź: 151 4845

Wersja PDF