Zadanie nr 1504251
Z sześciu odcinków długości 1,3,5,6,7,9 wybieramy losowo trzy. Oblicz prawdopodobieństwo że można z nich zbudować trójkąt.
Rozwiązanie
Jeżeli za zdarzenia elementarne przyjmiemy trzyelementowe zbiory wylosowanych liczb, to mamy
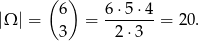
Z trzech odcinków można zbudować trójkąt jeżeli suma długości każdych dwóch jest większa od długości trzeciego. Zastanówmy się jakie trójki będą dobre w naszej sytuacji. Żeby się nie pogubić będziemy myśleć od najmniejszej z wylosowanych liczb, do największej.
Na pewno wśród wylosowanych liczb nie może być 1 (bo w sumie z mniejszą z pozostałych dwóch liczb nie da liczby większej od trzeciej). Jeżeli wylosujemy 3 i 5, lub 3 i 6, to trzecia liczba nie może być równa 9. Mamy 3 dobre trójki tej postaci
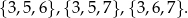
Jeżeli wylosujemy 3 i 7, to trzecia liczba musi być równa 9. Daje nam to trójkę 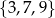 .
.
Pozostało rozważyć trójki, w których nie ma ani 1 ani 3. Każda z takich trójek jest OK i jest ich
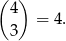
W sumie mamy więc
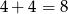
trójkątów i prawdopodobieństwo wynosi
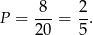
Odpowiedź: 

