Zadanie nr 1522186
W wazonie stoi 12 czerwonych i 8 żółtych róż. Pani Krystyna wyjęła losowo dwie róże z wazonu. Oblicz prawdopodobieństwo, że wśród wybranych kwiatów jest przynajmniej jedna róża żółta.
Rozwiązanie
Sposób I
Dwie róże z wazonu możemy wyjąć na
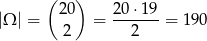
sposobów. Dwie róże żółte możemy wybrać na
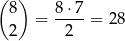
sposobów, a jedną żółtą i jedną czerwoną na
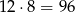
sposobów. Interesujące nas prawdopodobieństwo jest więc równe
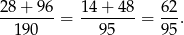
Sposób II
Jak poprzednio za zdarzenia elementarne przyjmujemy nieuporządkowane pary wybranych kwiatów, czyli
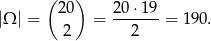
Zamiast liczyć prawdopodobieństwo szukanego zdarzenia policzymy prawdopodobieństwo zdarzenia przeciwnego, czyli że Pani Krystyna wyciągnęła dwie róże czerwone. Może zrobić to na
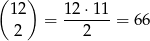
sposobów. Interesujące nas prawdopodobieństwo jest więc równe
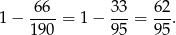
Sposób III
W wazonie znajduje się łącznie 20 kwiatów, a Pani Krystyna wyciąga dwa z nich (bez zwracania) zatem może to zrobić na
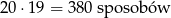
(tym razem uwzględniamy kolejność wybieranych kwiatów). Zdarzenia sprzyjające możemy podzielić na dwa: takie, w których Pani Krystyna wyciągnęła dokładnie jedną żółtą różę i takie, że że wyciągnęła dwie żółte róże. Najpierw policzmy na ile sposobów może wyciągnąć dokładnie jedną żółtą różę
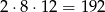
(żółtą różę możemy wybrać na 8 sposobów, a drugiego kwiatka na 12 sposobów, potem musimy ustalić czy żółta róża ma być pierwsza, czy druga).
Teraz policzmy na ile sposobów może wybrać dwie żółte róże
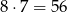
(Pierwszą żółtą różę możemy wybrać na 8 sposobów, a druga na 7). Zatem szukane prawdopodobieństwo jest równe
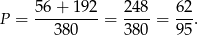
Sposób IV
Zamiast liczyć prawdopodobieństwo szukanego zdarzenia policzymy prawdopodobieństwo zdarzenia przeciwnego, czyli że Pani Krystyna wyciągnęła dwie róże czerwone (tak jak w poprzednim sposobie uwzględniamy kolejność wyciągniętych kwiatów). Może zrobić to na
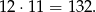
Zatem prawdopodobieństwo tego zdarzenia wynosi
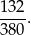
Czyli szukane prawdopodobieństwo wynosi
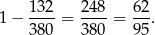
Odpowiedź: