Zadanie nr 1942094
Jedenastu panów, wśród których są 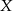 ,
, 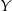 i
i 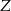 , ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że pan
, ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że pan 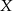 będzie stał obok pana
będzie stał obok pana 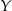 i pan
i pan 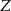 nie będzie stał obok pana
nie będzie stał obok pana 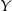 .
.
Rozwiązanie
Wszystkich możliwych ustawień 11 osób jest 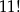 . Zatem
. Zatem
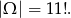
Policzmy liczbę zdarzeń sprzyjających. Parę sąsiednich miejsc dla panów 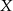 i
i 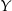 możemy wybrać na 10 sposobów (1,2 lub 2,3 itd.). Jak już są te miejsca wybrane, to mamy dwie możliwości ich ustawienia. Jest zatem 20 możliwości ustawienia panów
możemy wybrać na 10 sposobów (1,2 lub 2,3 itd.). Jak już są te miejsca wybrane, to mamy dwie możliwości ich ustawienia. Jest zatem 20 możliwości ustawienia panów 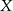 i
i 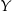 . Aby policzyć ile jest możliwości ustawienia pana
. Aby policzyć ile jest możliwości ustawienia pana 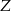 , rozważmy przypadki.
, rozważmy przypadki.
Jeżeli pan 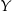 stoi z brzegu, tzn. na pierwszym lub 11 miejscu, to pan
stoi z brzegu, tzn. na pierwszym lub 11 miejscu, to pan 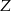 może stanąć na dowolnym z pozostałych 9 miejsc. Pozstałe osoby też ustawiamy dowolnie. Jest więc
może stanąć na dowolnym z pozostałych 9 miejsc. Pozstałe osoby też ustawiamy dowolnie. Jest więc
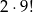
takich ustawień.
Jeżeli Pan 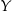 nie stoi na brzegu (jak już wiemy jest 18 takich ustawień), to pan
nie stoi na brzegu (jak już wiemy jest 18 takich ustawień), to pan 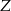 nie może stać obok niego, więc ma do wyboru 8 miejsc. Pozostałe osoby ustawiamy dowolnie. Jest
nie może stać obok niego, więc ma do wyboru 8 miejsc. Pozostałe osoby ustawiamy dowolnie. Jest
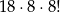
takich ustawień. Zatem
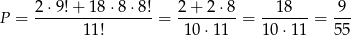
Odpowiedź: