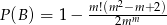Zadanie nr 2464870
Rozmieszczamy 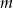 różnych listów w
różnych listów w 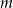 rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że:
rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że:
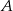 – co najmniej jedna skrytka jest pusta?
– co najmniej jedna skrytka jest pusta? 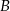 – co najmniej dwie skrytki są puste?
– co najmniej dwie skrytki są puste?
Rozwiązanie
Każdemu listowi przyporządkowujemy numer skrzynki, czyli
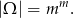
- Łatwiej jest policzyć prawdopodobieństwo zdarzenia przeciwnego, czyli takiego, że wszystkie skrzynki są zajęte. Skoro listów jest tyle samo co skrzynek, są to po prostu permutacje listów i mamy
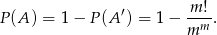
Odpowiedź: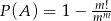
- Tak jak poprzednio, liczymy prawdopodobieństwo zdarzenia przeciwnego. Wiemy już, że jest
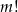 sytuacji, gdy wszystkie skrzynki są zajęte. Musimy jeszcze policzyć sytuacje, gdy dokładnie jedna jest wolna. Wolną skrytkę możemy wybrać na
sytuacji, gdy wszystkie skrzynki są zajęte. Musimy jeszcze policzyć sytuacje, gdy dokładnie jedna jest wolna. Wolną skrytkę możemy wybrać na 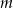 sposobów. Do tego na
sposobów. Do tego na 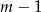 sposobów możemy wybrać skrzynkę, w której będą dwa listy. Które dwa? – to możemy wybrać na
sposobów możemy wybrać skrzynkę, w której będą dwa listy. Które dwa? – to możemy wybrać na 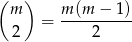
sposobów. Pozostałe
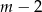 listów umieszczamy w
listów umieszczamy w 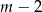 pozostałych skrzynkach permutując ich kolejność. Szukane prawdopodobieństwo wynosi więc
pozostałych skrzynkach permutując ich kolejność. Szukane prawdopodobieństwo wynosi więc 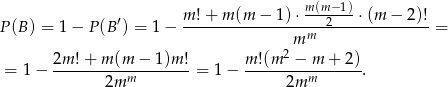
Odpowiedź: