/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 3536008

Dodaj do ulubionych
Dodaj do rozwiązanych

Grupę siedmiu osób, w których są trzy dziewczynki i czterech chłopców ustawiamy w rzędzie jeden za drugim. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie dziewczynki nie stoją bezpośrednio za sobą.

Rozwiązanie

Wszystkich możliwości ustawienia danych 7 osób jest

|Ω | = 7!

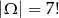
Sposób I

Każde ustawienie osób spełniające warunki zadania musi mieć jedną z postaci (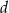d – dziewczynka, c – chłopiec):

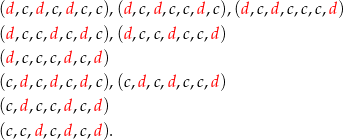
(d,c,d,c,d ,c,c),(d ,c,d ,c,c,d ,c),(d,c,d,c,c,c,d) (d,c,c,d,c,d,c),(d ,c,c,d ,c,c,d ) (d,c,c,c,d,c,d) (c,d,c,d,c,d,c),(c,d,c,d ,c,c,d ) (c,d,c,c,d,c,d) (c,c,d,c,d,c,d).

W każdej z tych 10 konfiguracji dziewczynki możemy wybrać na 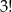3! sposobów, chłopców na 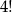4! sposobów. Interesujące nas prawdopodobieństwo jest więc równe

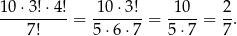
10-⋅3!⋅4!- 10-⋅3!- -10- 2- 7 ! = 5⋅6 ⋅7 = 5⋅ 7 = 7 .

Sposób II

Tym razem spróbujmy wypisać złe konfiguracje. Jest 5 konfiguracji:

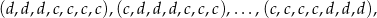
(d,d,d,c,c,c,c),(c,d,d,d ,c,c,c),...,(c,c,c,c,d,d,d),

w których wszystkie 3 dziewczynki stoją bezpośrednio za sobą. Wypiszemy teraz konfiguracje, w których dwie dziewczynki stoją za sobą, a trzecia nie stoi obok nich:

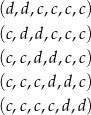
(d ,d,c,c,c,c) (c,d ,d,c,c,c) (c,c,d,d ,c,c) (c,c,c,d,d ,c) (c,c,c,c,d,d )

Łatwo sprawdzić, że w każdym z 5 powyższych przypadków są 4 sposoby dopisania brakującej trzeciej dziewczynki tak, aby nie stała obok dwóch dziewczynek. W sumie jest więc

5 ⋅4 = 20

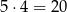
takich konfiguracji. W każdym z 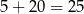5 + 20 = 25 przypadków chłopców możemy wybrać na 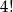4! sposobów, a dziewczynki na 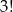3 ! sposobów. Interesujące nas prawdopodobieństwo jest więc równe

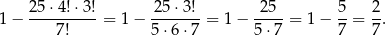
1 − 2-5⋅4-!⋅3! = 1 − -25⋅-3! = 1 − -25- = 1− 5-= 2. 7! 5 ⋅6 ⋅7 5 ⋅7 7 7

 
Odpowiedź: 27

Wersja PDF