Zadanie nr 3583629
Oblicz prawdopodobieństwo, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 4.
Rozwiązanie
Za zdarzenia elementarne przyjmijmy ciągi wyników, czyli
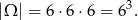
Policzmy teraz, ile jest zdarzeń sprzyjających.
Zauważmy najpierw, że kwadrat liczby całkowitej zawsze daje resztę 1 lub 0 przy dzieleniu przez 4. Rzeczywiście, jeżeli liczba jest parzysta to jej kwadrat dzieli się przez 4, a więc daje resztę 0. Jeżeli natomiast liczba  jest nieparzysta to
jest nieparzysta to 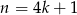 lub
lub 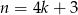 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 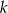 . Mamy wtedy odpowiednio
. Mamy wtedy odpowiednio
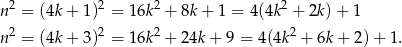
Zatem w obu przypadkach 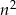 daje resztę 1 przy dzieleniu przez 4.
daje resztę 1 przy dzieleniu przez 4.
Teraz pora pomyśleć w jaki sposób suma kwadratów trzech liczb
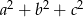
może dawać liczbę podzielną przez 4. Zauważmy, że żadna z tych liczb nie może być nieparzysta, bo w takiej sytuacji, patrząc na reszty mamy co najmniej jedną jedynkę, ale mamy tylko 3 liczby, więc suma reszt nie może dzielić się przez 4. Zatem rzeczywiście wszystkie liczby muszą być parzyste i mamy
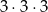
zdarzeń sprzyjających (na kostce są 3 liczby parzyste). Prawdopodobieństwo jest równe
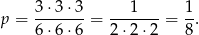
Odpowiedź: 

