/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 3830664

Dodaj do ulubionych
Dodaj do rozwiązanych

Przy okrągłym stole zasiada losowo 8 osób, a wśród nich rodzice z dwojgiem dzieci. Jakie jest prawdopodobieństwo tego, że dzieci usiądą bezpośrednio między rodzicami?

Rozwiązanie

Sposób I

Wszystkich możliwych usadzeń przy stole jest 8!, jednak niektóre z nich są nieodróżnialne, bo różnią się tylko cyklicznym przesunięciem (obrót wokół środka stołu). Dla każdego usadzenia jest osiem takich obrotów (łącznie z nim samym). Czyli odróżnialnych usadzeń jest

8! |Ω | = 8 = 7!

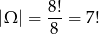
Dzieci mogą usiąść między rodzicami na 4 sposoby (tata, 1 dziecko, 2, dziecko, mama, itd.). Pozostałe 4 osoby mogą siedzieć dowolnie, czyli na 4! sposobów. Mamy zatem

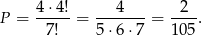
4 ⋅4! 4 2 P = ----- = ------- = ---. 7 ! 5 ⋅6 ⋅7 105

Sposób II

Tym razem nie bawmy się w obrócone ustawienia i przyjmijmy

|Ω | = 8!.

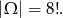
Zdarzenia sprzyjające liczymy jak poprzednio, rodziców z dziecmi możemy usadzić na 4 sposoby, resztę towarzystwa na 4! sposobów. Cały układ możemy jednak umieścić na 8 sposobów przy stole (obracając), więc

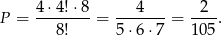
P = 4⋅4-!⋅8-= --4----= -2--. 8 ! 5⋅6 ⋅7 105

 
Odpowiedź: -2- 105

Wersja PDF