/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 4155091

Dodaj do ulubionych
Dodaj do rozwiązanych

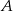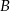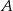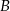W jadalni znajduje się okrągły stół, przy którym może usiąść 6 osób. Pod ścianą stoi ława, na której również może usiąść 6 osób. Do jadalni wchodzi 6 osób, które najpierw w sposób losowy siadają przy stole, a następnie na ławie. Które z prawdopodobieństw jest większe: prawdopodobieństwo tego, że A i B będą sąsiadami, siadając przy stole, czy prawdopodobieństwo tego, że A i B będą sąsiadami, siadając na ławie?

Rozwiązanie

Policzmy najpierw prawdopodobieństwo, że będą są sąsiadami przy stole. Wszystkich możliwych rozmieszczeń przy stole jest

6!.

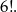
Natomiast sytuacji sprzyjających jest

2 ⋅6 ⋅4!

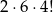
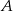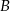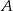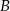(dwa miejsca jakie A i B zajmą możemy wybrać na 6 sposobów, pozostałe osoby możemy rozsadzić na 4! sposobów, no i musimy jeszcze uwzględnić to że A i B mogą zamienić się miejscami). Zatem prawdopodobieństwo wynosi

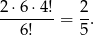
2⋅6-⋅4!- 2- 6 ! = 5.

Teraz policzmy prawdopodobieństwo, że będą sąsiadami siedząc na ławie. Znowu wszystkie osoby możemy posadzić na

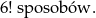
6 ! sposob ów .

Natomiast sytuacji sprzyjających jest

2 ⋅5 ⋅4!

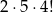
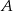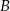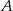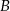(dwa sąsiednie miejsca dla A i B można wybrać na 5 sposobów, kolejność w jakiej usiądą A i B na dwa sposoby, a pozostałe 4 osoby siadają dowolnie). Zatem prawdopodobieństwo wynosi

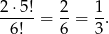
2⋅5-!= 2-= 1. 6! 6 3

 
Odpowiedź: Prawdopodobieństwo jest większe gdy siadają przy stole.

Wersja PDF