/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 4174437

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz prawdopodobieństwo, że w rzucie pięcioma sześciennymi kostkami do gry otrzymamy sumę oczek różną od 28.

Rozwiązanie

Jeżeli za zdarzenia elementarne przyjmiemy uporządkowane piątki wyrzuconych oczek, to mamy

|Ω | = 65.

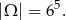
Powinno być jasne, że o wiele łatwiej jest policzyć liczbę możliwości otrzymania sumy oczek równej 28 niż sumy różnej od 28. Innym słowy liczymy prawdopodobieństwo zdarzenia przeciwnego.

Przy pięciu kostkach maksymalna suma oczek to 30, więc sumę 28 możemy otrzymać tylko po wyrzuceniu 4 szóstek i jednej czwórki, lub 3 szóstek i 2 piątek. Układów z jedną czwórką jest 5 (bo czwórka może być na jednej z 5 kostek). Układy z 2 piątkami możemy wypisać

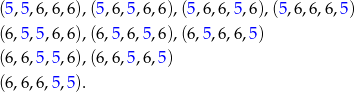
(5,5,6,6,6),(5,6,5,6,6 ),(5 ,6,6,5,6),(5,6,6,6,5) (6,5,5,6,6),(6,5,6,5,6 ),(6 ,5,6,6,5) (6,6,5,5,6),(6,6,5,6,5 ) (6,6,6,5,5).

A jeżeli ktoś nie chce wypisywać, to jest tych układów tyle ile możliwości wybrania 2 miejsc dla piątek spośród 5 miejsc, czyli

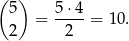
( ) 5 = 5⋅-4 = 10. 2 2

Zatem prawdopodobieństwo zdarzenia przeciwnego wynosi

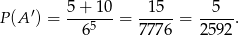
5+ 10 15 5 P(A ′) = ---5---= -----= -----. 6 7776 2592

Zatem

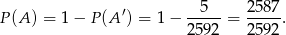
′ 5 258 7 P (A ) = 1− P(A ) = 1− 2592-= 259-2.

Uwaga. Mogło być kuszące przyjęcie za zdarzenia elementarne nieuporządkowanych piątek wyrzuconych oczek, czyli nie odróżnianie wyniku 1,1,1,1,2 od wyniku 2,1,1,1,1. To jednak jest źle, bo takie zdarzenia elementarne nie są jednakowo prawdopodobne (czyli nie są elementarne). Np. wynik 1,1,1,1,1 można otrzymać tylko na jeden sposób, podczas gdy wynik 1,1,1,1,2 uzyskamy z 5 różnych układów kostek. Uwzględniając kolejność otrzymanych wyników (czyli rozróżniając kostki) pozbyliśmy się tego problemu.  
Odpowiedź: 22558972

Wersja PDF