Zadanie nr 4213335
Do woreczka wrzucono 3 monety 5 złotowe, 4 monety 2 złotowe, 2 monety 1 złotowe oraz 8 monet 50 groszowych. Karol losowo wyjmuje z woreczka 10 monet. Jakie jest prawdopodobieństwo, że wylosuje w ten sposób co najmniej 10 zł? Wynik podaj z dokładnością do trzech miejsc po przecinku.
Rozwiązanie
Aby nie pomylić się w liczeniu zdarzeń załóżmy, że odróżniamy od siebie monety, czyli w sumie w woreczku jest
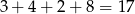
monet oraz
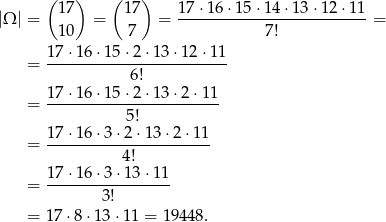
Teraz musimy policzyć zdarzenia sprzyjające, ale zamiast to robić policzymy zdarzenia sprzyjające zdarzeniu przeciwnemu, czyli sytuacji, gdy otrzymana kwota jest mniejsza niż 10.
Liczymy najpierw układy, w których jest 5-ka. Oczywiście musi być dokładnie jedna oraz nie może być 2-ki, bo jeżeli jest 5 i 2, to suma monet to co najmniej
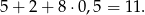
Z tych samych powodów nie może być 1-ki, bo
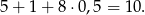
W takim razie jedyny układ z 5-ką to
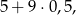
ale on też nie jest możliwy, bo jest tylko 8 monet 50-groszowych.
Możemy więc założyć, ze największe nominały to 2-ki. Maksymalnie mogą być 3, bo
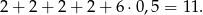
Jeżeli są 3, to w sumie dają 6 zł i jedyny możliwy układ to
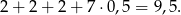
Od razu liczymy ile jest odpowiadających zdarzeń sprzyjających. 3 dwójki możemy wybrać na
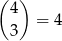
sposoby, a 7 50 groszówek na
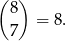
W sumie jest więc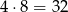 
takich zdarzeń.
Jeżeli natomiast są 2 dwójki, to maksymalnie mogą być 2 jedynki, co daje trzy możliwe układy
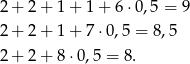
Dwie dwójki możemy wybrać na
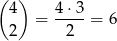
sposobów, więc każdemu z powyższych zdarzeń odpowiada odpowiednio
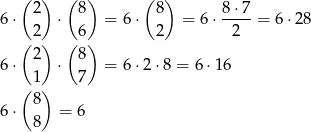
zdarzeń sprzyjających. W sumie daje to
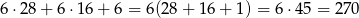
takich zdarzeń.
Mamy ponadto dwie konfiguracje z 1 dwójką.
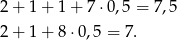
Każdej z powyższych konfiguracji odpowiada odpowiednio
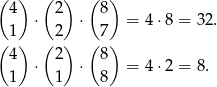
W sumie daje to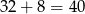 
zdarzeń sprzyjających.
Teraz liczymy konfiguracje, gdy największą monetą jest złotówka. Jest tylko jeden taki układ
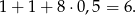
i dopowiada mu dokładnie jedno zdarzenie sprzyjające.
Ponieważ 50 groszówek jest tylko 8, nie ma już innych możliwości i prawdopodobieństwo zdarzenia przeciwnego jest równe
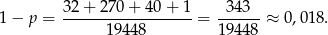
Czyli
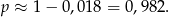
Odpowiedź: 0,982
