/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 4555953

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia: 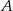A – na każdej kostce wypadła inna liczba oczek, 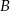B – suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia A ∖ B .

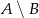Rozwiązanie

Jeżeli za zdarzenia elementarne przyjmiemy pary 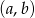(a,b) (uwzględniamy kolejność) to

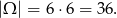
|Ω | = 6 ⋅6 = 36 .

Zdarzenia 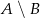A ∖ B , to wyniki, w których na każdej kostce są inne liczby oczek, oraz suma oczek jest równa co najmniej 6. Zatem sprzyjające wyniki to

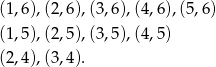
(1,6),(2,6),(3,6 ),(4 ,6),(5,6) (1,5),(2,5),(3,5 ),(4 ,5) (2,4),(3,4).

Wypisaliśmy tylko te wyniki 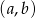(a,b) , w których 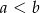a < b . Jest oczywiście tyle samo wyników z 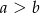a > b (trzeba zamienić obie liczby miejscami). Zatem

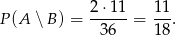
2 ⋅11 11 P(A ∖B ) = ------= --. 36 18

 
Odpowiedź: 11 18

Wersja PDF