/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 4592903

Dodaj do ulubionych
Dodaj do rozwiązanych

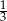W jednej urnie jest 5 kul białych i pewna liczba kul czarnych, w drugiej zaś 6 kul czarnych i pewna liczba kul białych. Z każdej urny losujemy po dwie kule. Prawdopodobieństwo wylosowania jednocześnie dwóch kul białych z pierwszej urny jest większe od 2 9 , a prawdopodobieństwo jednoczesnego wylosowania dwóch kul czarnych z drugiej urny jest większe od 1 3 . W której urnie jest więcej kul białych, a w której czarnych?

Rozwiązanie

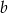Powiedzmy, że w pierwszej urnie jest c kul czarnych, a w drugiej b kul białych. Zatem możliwości wyciągnięcia 2 kul z urn jest odpowiednio

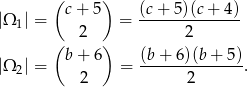
( ) |Ω1| = c + 5 = (c-+-5)(c+--4) 2 2 (b + 6) (b + 6)(b + 5) |Ω2| = = ---------------. 2 2

Zdarzeń sprzyjających jest odpowiednio

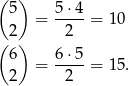
( ) 5 = 5⋅-4 = 10 2 2 ( 6) 6⋅ 5 = ---- = 15. 2 2

Mamy więc nierówności

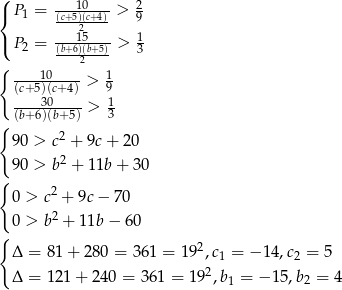
( ---10--- 2 { P 1 = (c+-5)(c+4)> 9 ( ---215--- 1 P 2 = (b+6)(b2+5) > 3 { 10 1 (c+5)(c+-4) > 9 ---30-----> 1 { (b+ 6)(b+5) 3 90 > c2 + 9c + 2 0 2 90 > b + 11b+ 30 { 2 0 > c + 9c − 70 0 > b2 + 1 1b− 60 { Δ = 81 + 280 = 361 = 1 92,c1 = − 14,c2 = 5 Δ = 121 + 24 0 = 361 = 192,b = − 15,b = 4 1 2

Zatem 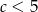c < 5 i b < 4 .  
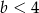Odpowiedź: W pierwszej urnie jest więcej kul białych, w drugiej czarnych

Wersja PDF