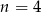/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 4968127

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru wszystkich trójwyrazowych ciągów o wyrazach ze zbioru 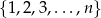{1 ,2,3,...,n} losujemy jeden ciąg.

  • Oblicz prawdopodobieństwo wylosowania ciągu rosnącego lub malejącego.
  • Dla jakiej liczby naturalnej n prawdopodobieństwo to jest równe 0,125?

Rozwiązanie

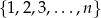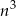Wszystkich ciągów trójwyrazowych o wyrazach ze zbioru { 1,2,3,...,n} jest n 3 (każdy z wyrazów możemy wybrać na n sposobów). Zatem

|Ω | = n3.
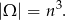
  • Jeżeli ciąg ma być rosnący lub malejący, to wszystkie wyrazy muszą być różne. Możliwości wyboru 3 różnych liczb ze zbioru 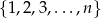{1,2,3,...,n } jest
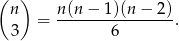
    (n ) n (n− 1)(n − 2) = ----------------. 3 6

    Tak wybrane liczby można ustawić w ciąg rosnący na dokładnie jeden sposób i w ciąg malejący na jeden sposób. Zdarzeń sprzyjających jest więc

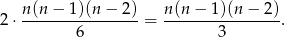
    2 ⋅ n(n-−-1-)(n−-2) = n-(n-−-1)(n-−-2). 6 3

    Stąd

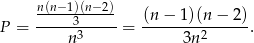
    n(n−1)(n−2) P = -----3----- = (n−--1)(n-−-2). n 3 3n 2

     
    Odpowiedź: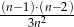 (n−1)⋅(n−-2)- 3n2

  • Musimy rozwiązać równanie
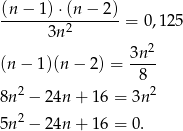
    (n-−-1)-⋅(n-−-2)-= 0,125 3n 2 3n2 (n − 1)(n − 2) = ---- 8 8n2 − 24n + 16 = 3n 2 2 5n − 24n + 16 = 0.

    Dalej,

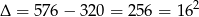
    2 Δ = 576− 320 = 2 56 = 16

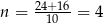    i jedyny naturalny pierwiastek to n = 24+1106 = 4 .  
    Odpowiedź: n = 4

Wersja PDF