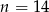Zadanie nr 7025718
W pojemniku znajduje się 28 kul, przy czym 
z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby 
prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
Rozwiązanie
Za zdarzenia elementarne przyjmujemy pary wylosowanych liczb, czyli
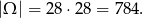
Policzmy zdarzenia sprzyjające. Mamy dwie możliwości: albo najpierw wylosowaliśmy kulę białą a potem czarną, albo odwrotnie. W sumie daje to nam
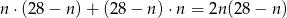
zdarzeń sprzyjających. Zatem prawdopodobieństwo jest równe
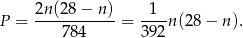
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół, zatem największą wartość prawdopodobieństwa otrzymamy w wierzchołku, czyli dla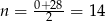 
(dokładnie w środku między pierwiastkami).
Odpowiedź: 
