Zadanie nr 7299956
Ze zbioru wszystkich liczb trzycyfrowych, które są podzielne przez 7 wybieramy losowo 5 różnych liczb. Oblicz prawdopodobieństwo tego, że jedną z tych liczb jest 546, a wśród pozostałych 4 liczb jest dokładnie jedna liczba mniejsza od 546. Wynik podaj w postaci ułamka nieskracalnego.
Rozwiązanie
Zacznijmy od ustalenia ile jest liczb trzycyfrowych podzielnych przez 7. Liczby te to
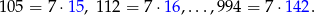
Liczb tych jest więc tyle, ile liczb od 15 do 142, a tych liczb z kolei jest tyle samo, co liczb od 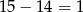 do
do 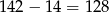 , czyli 128.
, czyli 128.
Liczbę liczb trzycyfrowych podzielnych przez 7 mogliśmy też wyliczyć ze wzoru na  -ty wyraz ciągu arytmetycznego. Dla urozmaicenia policzymy w ten sposób ile jest liczb trzycyfrowych podzielnych przez 7 i mniejszych od 546. Liczby te są kolejnymi wyrazami ciągu arytmetycznego o różnicy 7:
-ty wyraz ciągu arytmetycznego. Dla urozmaicenia policzymy w ten sposób ile jest liczb trzycyfrowych podzielnych przez 7 i mniejszych od 546. Liczby te są kolejnymi wyrazami ciągu arytmetycznego o różnicy 7:
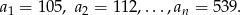
Ze wzoru na  -ty wyraz ciągu arytmetycznego mamy
-ty wyraz ciągu arytmetycznego mamy
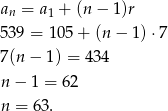
Wiemy zatem, że jest 128 liczb trzycyfrowych podzielnych przez 7, z czego 63 są mniejsze od 546, a 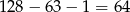 z nich jest większa od 546.
z nich jest większa od 546.
Za zdarzenia elementarne przyjmijmy 5-elementowe zbiory wylosowanych liczb. Zatem
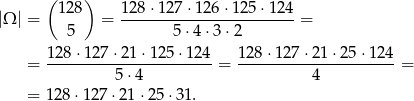
Liczymy teraz liczbę zdarzeń sprzyjających. Wiemy, że jedną z wylosowanych liczb ma być 546 - tu nie mamy żadnego wyboru. Wiemy też, że jedna z liczb musi być mniejsza od 546 – możemy ją wybrać na 63 sposoby. Pozostałe 3 liczby musimy wybrać ze zbioru liczb większych od 546 – możemy to zrobić na
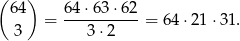
sposoby.
Prawdopodobieństwo jest więc równe
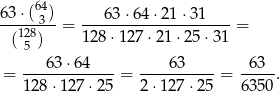
Otrzymany ułamek jest nieskracalny, bo 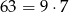 , a 6350 nie dzieli się ani przez 3, ani przez 7.
, a 6350 nie dzieli się ani przez 3, ani przez 7.
Odpowiedź: