Zadanie nr 7669572
Niech 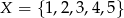 i
i 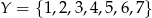 . Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji
. Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji 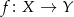 jest dwuelementowy.
jest dwuelementowy.
Rozwiązanie
Aby zdefiniować funkcję 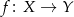 musimy określić 5 wartości funkcji
musimy określić 5 wartości funkcji 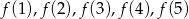 . Każdą z tych liczb możemy wybrać na 7 sposobów, więc
. Każdą z tych liczb możemy wybrać na 7 sposobów, więc
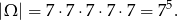
Policzmy teraz ile jest funkcji, których zbiór wartości składa się dokładnie z dwóch elementów.
Sposób I
Dwa elementy ze zbioru 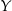 możemy wybrać na
możemy wybrać na
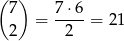
sposobów. To jednak jeszcze nie koniec, bo musimy ustalić, którym argumentom przyporządkujemy które wartości. Powiedzmy, że ze zbioru 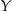 wybraliśmy wartości
wybraliśmy wartości 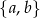 . Aby zdefiniować funkcję o wartościach
. Aby zdefiniować funkcję o wartościach  i
i 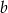 wystarczy ustalić, na których argumentach ma przyjąć wartość
wystarczy ustalić, na których argumentach ma przyjąć wartość  (wtedy na pozostałych musi być wartość
(wtedy na pozostałych musi być wartość 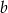 ). Możliwości wyboru mamy tyle, ile jest podzbiorów zbioru
). Możliwości wyboru mamy tyle, ile jest podzbiorów zbioru 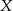 , które nie są puste i nie są całym zbiorem, czyli
, które nie są puste i nie są całym zbiorem, czyli
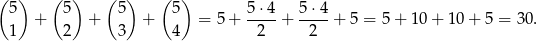
Zatem jest 30 funkcji o ustalonych wartościach 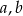 , czyli w sumie jest
, czyli w sumie jest
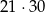
zdarzeń sprzyjających i prawdopodobieństwo wynosi
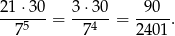
Sposób II
Tak jak poprzednio ustalamy, że jest
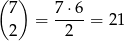
możliwości wyboru dwóch liczb 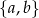 ze zbioru
ze zbioru 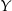 .
.
Jeżeli  i
i 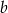 mamy ustalone, to każda z wartości
mamy ustalone, to każda z wartości 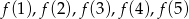 może być jedną z tych liczb, więc jest
może być jedną z tych liczb, więc jest
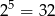
funkcji, których wartości zawierają się w zbiorze 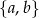 . Jednak nie wszystkie z nich spełniają warunki zadania: trzeba odjąć dwie funkcje stałe, które przyjmują wyłącznie wartość
. Jednak nie wszystkie z nich spełniają warunki zadania: trzeba odjąć dwie funkcje stałe, które przyjmują wyłącznie wartość  lub wartość
lub wartość 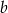 . Zatem w sumie jest 30 „dobrych” funkcji, co daje
. Zatem w sumie jest 30 „dobrych” funkcji, co daje
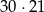
zdarzeń sprzyjających. Prawdopodobieństwo liczymy jak poprzednio
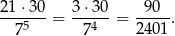
Odpowiedź: