Zadanie nr 7978714
Oblicz prawdopodobieństwo otrzymania dokładnie dwóch jedynek lub trzech szóstek w doświadczeniu losowym, polegającym na pięciokrotnym rzucie symetryczną sześcienną kostką do gry.
Rozwiązanie
Niech 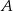 oznacza zdarzenie polegające na otrzymaniu dokładnie dwóch jedynek, a
oznacza zdarzenie polegające na otrzymaniu dokładnie dwóch jedynek, a 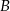 zdarzenie polegające na otrzymaniu dokładnie trzech szóstek.
zdarzenie polegające na otrzymaniu dokładnie trzech szóstek.
Sposób I
Za zdarzenia sprzyjające przyjmijmy ciągi długości 5 otrzymanych liczb oczek. Mamy zatem
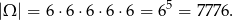
Policzmy zdarzenia sprzyjające zdarzeniu 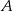 . W zdarzeniach tych mają być dokładnie dwie jedynki – ich miejsca możemy wybrać na
. W zdarzeniach tych mają być dokładnie dwie jedynki – ich miejsca możemy wybrać na
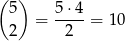
sposobów. Na każdym z pozostałych trzech miejsc może być jedna z liczb: 2,3,4,5,6. Daje to (zasada mnożenia)
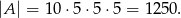
Podobnie obliczamy liczbę zdarzeń sprzyjających zdarzeniu 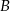 . Miejsca dla 6-tek możemy wybrać na
. Miejsca dla 6-tek możemy wybrać na
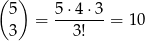
sposobów, do tego na każdym z pozostałych miejsc mamy 5 możliwości, czyli jest
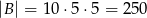
zdarzeń sprzyjających 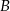 .
.
To co mamy obliczyć to prawdopodobieństwo zdarzenia 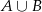 , zanim to jednak zrobimy obliczmy ile jest zdarzeń sprzyjających zdarzeniu
, zanim to jednak zrobimy obliczmy ile jest zdarzeń sprzyjających zdarzeniu 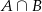 . W zdarzeniach takich musimy mieć dwie jedynki i trzy szóstki. Miejsca jedynek możemy wybrać na
. W zdarzeniach takich musimy mieć dwie jedynki i trzy szóstki. Miejsca jedynek możemy wybrać na
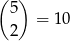
sposobów, więc 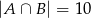 . Stąd
. Stąd
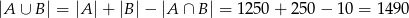
i prawdopodobieństwo wynosi
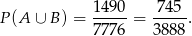
Sposób II
Korzystamy ze schematu Bernoullego. Jeżeli za sukces uznamy otrzymanie jedynki przy rzucie kostką, to prawdopodobieństwo sukcesu jest równe
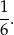
Prawdopodobieństwo dwóch sukcesów w 5 próbach jest równe
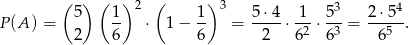
Podobnie obliczamy prawdopodobieństwo zdarzenia 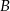 – tym razem za sukces przyjmijmy otrzymanie szóstki. Prawdopodobieństwo trzech sukcesów jest równe
– tym razem za sukces przyjmijmy otrzymanie szóstki. Prawdopodobieństwo trzech sukcesów jest równe
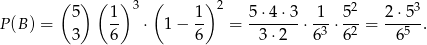
Mamy obliczyć 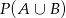 , nie jest to jednak
, nie jest to jednak 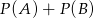 , bo zdarzenia te nie są rozłączne. Zastanówmy się jakie jest prawdopodobieństwo
, bo zdarzenia te nie są rozłączne. Zastanówmy się jakie jest prawdopodobieństwo 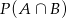 . W zdarzeniach tego typu musimy wylosować 3 szóstki i 2 jedynki. Miejsca dla 2 jedynek możemy wybrać na
. W zdarzeniach tego typu musimy wylosować 3 szóstki i 2 jedynki. Miejsca dla 2 jedynek możemy wybrać na
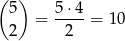
sposobów i jest to jedyna możliwość manewru, na pozostałych 3 miejscach muszą być 6-ki. Zatem
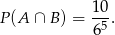
Mamy stąd
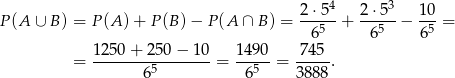
Odpowiedź: