/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 8032062

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz prawdopodobieństwo tego, że przy czterokrotnym rzucie kostką, 3 kolejne wyniki utworzą ciąg geometryczny.

Rozwiązanie

Za zdarzenia sprzyjające przyjmijmy uporządkowane ciągi wyrzuconych oczek. Mamy zatem

|Ω | = 64.

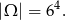
Możliwe 3-elementowe ciągi geometryczne utworzone z liczb od 1 do 6 są następujące

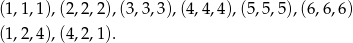
(1,1,1),(2,2,2),(3,3,3 ),(4 ,4,4),(5,5,5),(6,6,6) (1,2,4),(4,2,1).

Pozostało ustalić na ile sposobów można te ciągi umieścić w 4–elementowych wynikach.

Jeżeli chodzi o ciągi stałe (o ilorazie 1), to każdy z nich może się pojawić na

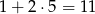
1 + 2 ⋅5 = 11

sposobów: 1 odpowiada ciągowi, którego wszystkie wyrazy są równe, pozostałe możliwości odpowiadają sytuacjom, gdy czwarta liczba jest różna od 3 pozostałych – można ją umieścić na 2 sposoby (na końcu lub początku).

Jeżeli chodzi natomiast o pozostałe dwa ciągi, to dla każdego z nich mamy 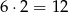6 ⋅2 = 12 możliwości – musimy dopisać jedną liczbę na początku lub końcu.

W sumie mamy więc

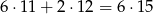
6 ⋅11 + 2 ⋅12 = 6 ⋅15

zdarzeń sprzyjających. Stąd

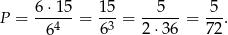
6 ⋅15 15 5 5 P = ------= ---= ------= --. 64 63 2⋅ 36 72

 
Odpowiedź: 5 72

Wersja PDF