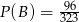Zadanie nr 9748129
Z szuflady, w której znajduje się 10 różnych par rękawiczek wybieramy losowo cztery rękawiczki. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwa zdarzeń:
A – wśród wylosowanych rękawiczek nie będzie pary,
B – wśród wylosowanych rękawiczek będzie dokładnie jedna para.
Rozwiązanie
Sposób I
Przyjmijmy, że zdarzenia elementarne to wybory nieuporządkowane czterech rękawiczek. W takiej sytuacji
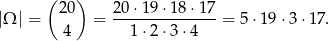
Zdarzenia sprzyjające do 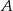 , to takie, w których każda z wybranych rękawiczek jest z innej pary. Takich zdarzeń sprzyjających jest
, to takie, w których każda z wybranych rękawiczek jest z innej pary. Takich zdarzeń sprzyjających jest
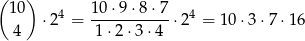
(najpierw wybieramy z którch par mają pochodzić rękawiczki, a w każdej parze mamy dwie możliwości wyboru rękawiczki). Zatem
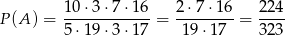
Zdarzenia sprzyjające do 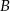 , to takie, w których mamy jedną parę i dwie rękawiczki z różnych par. Mamy zatem
, to takie, w których mamy jedną parę i dwie rękawiczki z różnych par. Mamy zatem
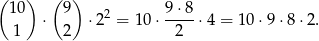
takich możliwości (wybieramy jedną parę, potem z pozostałych dwie pary i w każdej z tych dwóch par mamy dwie możliwości wyboru rękawiczki). Mamy zatem
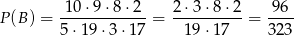
Prawdopodobieństwo 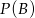 mogliśmy policzyć trochę prościej, licząc prawdopodobieństwo
mogliśmy policzyć trochę prościej, licząc prawdopodobieństwo 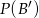 zdarzenia przeciwnego. Zdarzenie
zdarzenia przeciwnego. Zdarzenie 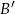 składa się z dwóch możliwości: że nie ma żadnej pary lub, że są dwie pary. Pierwsze ze zdarzeń to zdarzenie
składa się z dwóch możliwości: że nie ma żadnej pary lub, że są dwie pary. Pierwsze ze zdarzeń to zdarzenie 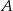 , a prawdopodbieństwo
, a prawdopodbieństwo 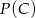 drugiego to
drugiego to
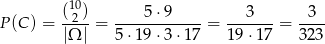
(wybieramy dwie pary z 10). Zatem
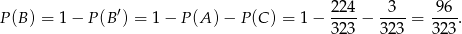
Sposób II
Tym razem za zdarzenia elementarne przyjmijmy uporządkowane czwórki rękawiczek. Mamy zatem
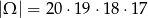
(pierwszą rękawiczkę możemy wybrać na 20 sposobów, drugą na 19 itd.). W zdarzeniach sprzyjających 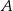 , po wybraniu rękawiczki z jakiejś pary, nie możemy już wybrać drugiej rękawiczki z tej pary, jest zatem
, po wybraniu rękawiczki z jakiejś pary, nie możemy już wybrać drugiej rękawiczki z tej pary, jest zatem
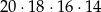
zdarzeń sprzyjających. Stąd
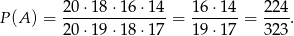
Policzmy teraz zdarzenia sprzyjające do 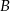 . Mamy
. Mamy 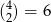 możliwości na to, które z wybranych 4 rękawiczek tworzą parę. Jeżeli to jest już ustalone (na których miejscach jest para), to te dwie rękawiczki tworzące parę możemy wybrać na
możliwości na to, które z wybranych 4 rękawiczek tworzą parę. Jeżeli to jest już ustalone (na których miejscach jest para), to te dwie rękawiczki tworzące parę możemy wybrać na 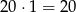 sposobów (pierwszą dowolnie, a druga musi być z kompletu). Pozostałe 2 rękawiczki możemy dobrać na
sposobów (pierwszą dowolnie, a druga musi być z kompletu). Pozostałe 2 rękawiczki możemy dobrać na 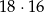 sposobów. Zatem
sposobów. Zatem
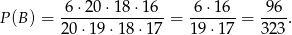
Odpowiedź: 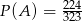 ,
,