Zadanie nr 3343064
Wykaż, że rozwiązaniem nierówności 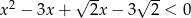 jest przedział
jest przedział 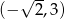 .
.
Rozwiązanie
Sposób I
Liczymy
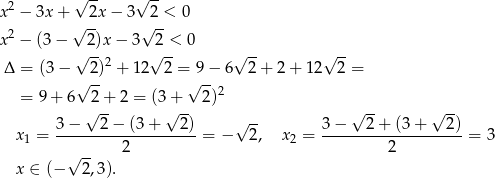
Sposób II
Zauważmy, że w danej nierówności można łatwo wyłączyć 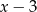 .
.
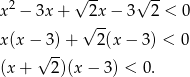
No i otrzymaliśmy zwykłą nierówność kwadratową, której rozwiązanie jest przedział 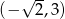 .
.
Sposób III
Jeżeli nie zauważmy, że 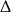 jest pełnym kwadratem, to otrzymamy rozwiązanie
jest pełnym kwadratem, to otrzymamy rozwiązanie
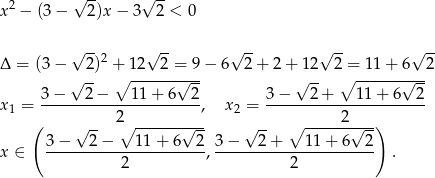
Teraz wystarczy sprawdzić, że lewy koniec tego przedziału to 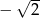 , a prawy to 3. Sprawdzamy
, a prawy to 3. Sprawdzamy
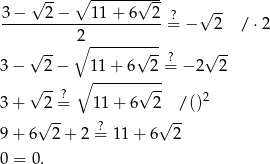
Podobnie sprawdzamy prawy koniec przedziału.
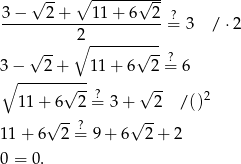
Sposób IV
Wiemy, że przedział 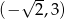 jest rozwiązaniem nierówności kwadratowej
jest rozwiązaniem nierówności kwadratowej
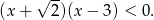
Wymnażając nawiasy mamy
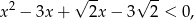
czyli dokładnie nierówność z treści zadania.

