/Szkoła średnia/Nierówności/Udowodnij.../Kwadratowe/1 literka

Zadanie nr 5989756

Dodaj do ulubionych
Dodaj do rozwiązanych

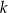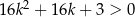Wykaż, że dla dowolnej liczby całkowitej k prawdziwa jest nierówność 16k 2 + 1 6k+ 3 > 0 .

Rozwiązanie

Próbujemy rozwiązać daną nierówność.

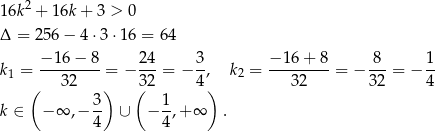
2 16k + 16k + 3 > 0 Δ = 256 − 4 ⋅3⋅ 16 = 64 − 1 6− 8 24 3 − 16 + 8 8 1 k1 = ---------= − ---= − -, k2 = ---------= − ---= − -- ( 3 2 ) (32 4) 32 32 4 3- 1- k ∈ − ∞ ,− 4 ∪ − 4 ,+∞ .

Zauważmy teraz, że w przedziale 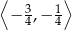⟨ 3 1⟩ − 4,− 4 nie ma żadnej liczby całkowitej, więc rzeczywiście każda liczba całkowita spełnia powyższą nierówność.

Wersja PDF