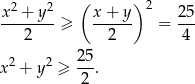/Szkoła średnia/Nierówności/Udowodnij.../Kwadratowe/2 literki

Zadanie nr 5387253

Dodaj do ulubionych
Dodaj do rozwiązanych

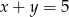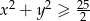Wykaż, że jeżeli x + y = 5 , to 2 2 25 x + y ≥ 2 .

Rozwiązanie

Sposób I

Podstawiamy w nierówności, która mamy wykazać 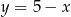y = 5 − x i przekształcamy ją w sposób równoważny.

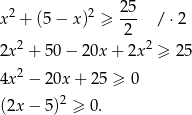
25 x2 + (5− x)2 ≥ --- / ⋅2 2 2x2 + 50 − 20x + 2x 2 ≥ 25 2 4x − 20x + 25 ≥ 0 (2x − 5)2 ≥ 0.

Otrzymana nierówność jest oczywiście spełniona, więc wyjściowa nierówność też musiała być prawdziwa.

Sposób II

Korzystamy z nierówności

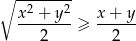
∘ -------- x2 + y2 x + y --------≥ ------ 2 2

pomiędzy średnią kwadratową i arytmetyczną. Mamy zatem

2 2 ( )2 x-+--y--≥ x-+-y- = 25- 2 2 4 2 2 25 x + y ≥ ---. 2
Wersja PDF