Zadanie nr 5838004
Wykaż, że dla każdej liczby rzeczywistej  większej od 2 i dla każdej liczby rzeczywistej
większej od 2 i dla każdej liczby rzeczywistej 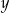 prawdziwa jest nierówność
prawdziwa jest nierówność 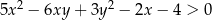 .
.
Rozwiązanie
Sposób I
Zauważmy, że lewą stronę nierówności możemy zapisać w postaci
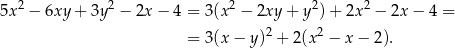
Wystarczy teraz uzasadnić, że wyrażenie w drugim nawiasie jest dodatnie. Rozkładamy je na czynniki
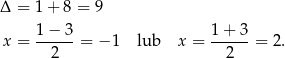
Zatem
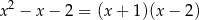
i widać, że wyrażenie to jest dodatnie dla 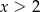 .
.
Sposób II
Tak jak poprzednio przekształcamy lewą stronę nierówności do postaci
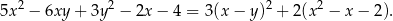
Dodatniość wyrażenia w drugim nawiasie dowodzimy jednak inaczej – sprowadzając ten trójmian do postaci kanonicznej
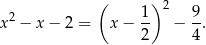
Jeżeli 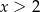 , to
, to
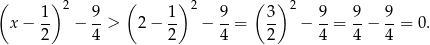
Sposób III
Zapiszmy lewą stronę nierówności jak funkcję kwadratową zmiennej 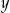
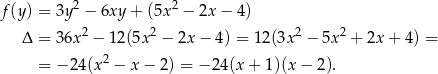
Widać teraz, że 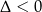 dla
dla 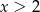 , czyli
, czyli
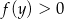
dla każdej wartości 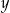 .
.

