Zadanie nr 9180074

Dana jest nierówność kwadratowa z parametrem :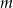

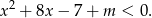
2 x + 8x− 7+ m < 0.

Wyznacz wszystkie wartości parametru 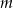, dla których przedział 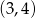zawiera się w zbiorze rozwiązań tej nierówności.
Uzasadnij, że jeżeli dla pewnej wartości parametru 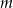nierówność ta ma rozwiązanie w przedziale 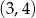, to ma ona w tym przedziale nieskończenie wiele rozwiązań.

Rozwiązanie

Zacznijmy od zauważenia, że wierzchołek paraboli 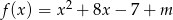ma pierwszą współrzędna równą 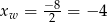. Zatem wykres lewej strony nierówności jest parabolą o ramionach skierowanych w górę i osi symetrii 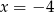. W szczególności parabola ta jest funkcją rosnącą na przedziale 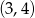. Zatem jej ujemność na tym przedziale sprowadza się do warunku 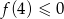(tu jest ważne, że przedział jest otwarty). Daje to nam nierówność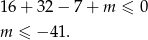
$1 6+ 32− 7+ m ≤ 0 m ≤ − 41 .$

Odpowiedź: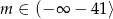
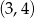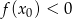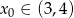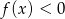Jak już zauważyliśmy w poprzednim podpunkcie, lewa strona nierówności rośnie na przedziale . To oznacza, że jeżeli dla pewnego to dla 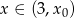, co oznacza, że nierówność ma nieskończenie wiele rozwiązań.