Zadanie nr 9427780
Udowodnij, że jeśli 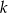 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 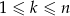 , to
, to 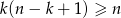 .
.
Rozwiązanie
Sposób I
Przekształćmy nierówność
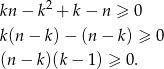
Z podanych założeń wyrażenia w obydwu nawiasach są nieujemne, co dowodzi żądanej nierówności.
Sposób II
Przekształcamy nierówność
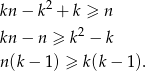
Jeżeli 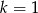 to nierówność jest oczywiście spełniona. Załóżmy więc, że
to nierówność jest oczywiście spełniona. Załóżmy więc, że 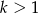 i możemy wtedy podzielić nierówność stronami przez
i możemy wtedy podzielić nierówność stronami przez 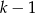 . Zostaje nierówność
. Zostaje nierówność
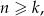
która jest spełniona na mocy podanych założeń.

