/Szkoła średnia/Nierówności/Udowodnij.../Kwadratowe/2 literki

Zadanie nr 9996229

Dodaj do ulubionych
Dodaj do rozwiązanych

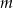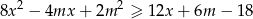Udowodnij, że dla każdej liczby rzeczywistej x i każdej liczby rzeczywistej m prawdziwa jest nierówność 8x2 − 4mx + 2m 2 ≥ 12x + 6m − 18 .

Rozwiązanie

Jeżeli zapiszemy daną nierówność w postaci

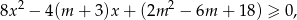
2 2 8x − 4(m + 3)x+ (2m − 6m + 18) ≥ 0,

to widać, że mamy do czynienia ze zwykłą nierównością kwadratową. Ramiona paraboli będącej wykresem lewej strony są skierowane w górę, więc wystarczy pokazać, że 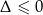Δ ≤ 0 . Liczymy

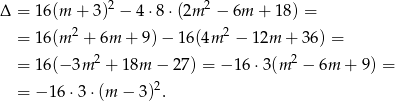
Δ = 16(m + 3)2 − 4⋅8 ⋅(2m 2 − 6m + 18) = 2 2 = 16(m + 6m + 9 )− 16 (4m − 12m + 36) = = 16(− 3m 2 + 18m − 27) = − 16 ⋅3(m 2 − 6m + 9) = = − 16⋅ 3⋅(m − 3)2.

Widać teraz, że rzeczywiście 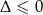Δ ≤ 0 .

Wersja PDF