/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2023/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 29 kwietnia 2023 Czas pracy: 100 minut
Wśród uczniów klas siódmych przeprowadzono ankietę. Jedno z pytań tej ankiety zamieszczono poniżej.

Każdy z uczniów wypełniających ankietę zaznaczył tylko jedną odpowiedź. Odpowiedź filmy przyrodnicze otrzymała o 2 głosy więcej niż odpowiedź żadne z wymienionych. Procentowy rozkład wszystkich udzielonych odpowiedzi uczniów przedstawiono na poniższym diagramie.
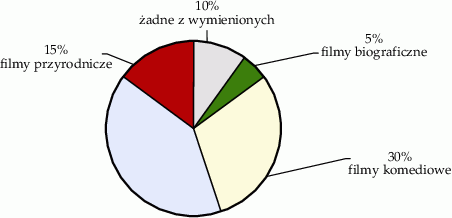
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Filmy komediowe wybrało 10 uczniów. | P | F |
| Liczba uczniów, którzy wybrali filmy fantasy była o 14 większa niż liczba uczniów, którzy wybrali filmy biograficzne. | P | F |
Poniżej zapisano trzy liczby:
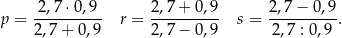
Który zapis przedstawia poprawnie uporządkowane liczby  od najmniejszej do największej?
od najmniejszej do największej?
A)  B)
B) 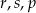 C)
C) 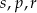 D)
D) 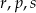
Spośród wszystkich liczb trzycyfrowych o sumie cyfr równej 7 wybrano liczbę największą i liczbę najmniejszą.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma wybranych liczb jest równa
A) 806 B) 716 C) 860 D) 707
Dane są cztery wyrażenia:
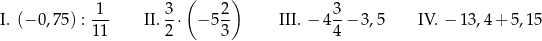
Wartość którego wyrażenia nie jest równa 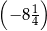 ?
?
A) I B) II C) III D) IV
Liczba 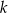 jest różnicą liczb 1423 i 1130. Czy liczba
jest różnicą liczb 1423 i 1130. Czy liczba 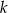 jest podzielna przez 3?
jest podzielna przez 3?
Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | cyfrą jedności liczby 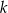 jest 3. jest 3. |
| B) | żadna z liczb 1423 i 1130 nie dzieli się przez 3. |
| C) | suma cyfr liczby 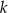 nie jest liczbą podzielną przez 3. nie jest liczbą podzielną przez 3. |
Dane są cztery liczby
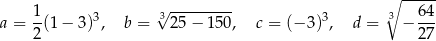
Które zdanie jest fałszywe?
A) Wszystkie liczby są ujemne.
B) Liczba 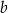 jest większa niż liczba
jest większa niż liczba  .
.
C) Liczba  jest o 23 mniejsza niż liczba
jest o 23 mniejsza niż liczba  .
.
D) Liczba 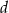 jest 3 razy mniejsza niż liczba
jest 3 razy mniejsza niż liczba  .
.
E) Liczba 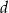 jest większa niż liczba
jest większa niż liczba 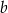 .
.
Dane są trzy liczby:
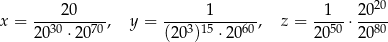
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dwie spośród liczb 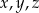 są większe od liczby są większe od liczby 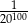 . . | P | F |
Różnica dwóch spośród liczb 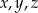 jest równa 0. jest równa 0. | P | F |
Na uszycie 120 jednakowych czapek w rozmiarze 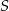 potrzeba tyle samo materiału, ile na uszycie 90 jednakowych czapek w rozmiarze
potrzeba tyle samo materiału, ile na uszycie 90 jednakowych czapek w rozmiarze 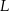 . Przyjmij, że na uszycie większej lub mniejszej liczby czapek potrzeba proporcjonalnie więcej lub mniej materiału.
. Przyjmij, że na uszycie większej lub mniejszej liczby czapek potrzeba proporcjonalnie więcej lub mniej materiału.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Na uszycie 160 czapek w rozmiarze 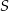 potrzeba tyle samo materiału, ile potrzeba na uszycie A/B czapek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie A/B czapek w rozmiarze 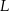 .
.
A) 150 B) 120
Na uszycie trzech czapek w rozmiarze 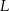 potrzeba tyle samo materiału, ile potrzeba na uszycie C/D czapek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie C/D czapek w rozmiarze 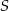 .
.
C) czterech D) pięciu
Dane są trzy liczby 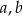 i
i  . Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Gdy  oraz
oraz  jest liczbą większą od 1, to suma
jest liczbą większą od 1, to suma 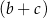 jest A/B .
jest A/B .
A) dodatnia B) ujemna
Gdy 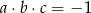 oraz
oraz  jest liczbą większą od zera, to iloczyn
jest liczbą większą od zera, to iloczyn 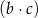 jest C/D .
jest C/D .
C) dodatni D) ujemny
Trzy koleżanki kupiły bilety autobusowe w tym samym automacie. Kamila kupiła 3 bilety 20–minutowe, 2 bilety 75–minutowe, jeden bilet 24–godzinny i zapłaciła za te bilety 28 zł. Justyna kupiła 2 bilety 20–minutowe, 3 bilety 75–minutowe, 4 bilety 24–godzinne i zapłaciła za te bilety 62 zł. Kasia kupiła jeden bilet 20–minutowy, jeden bilet 75–minutowy i jeden bilet 24–godzinny. Ile Kasia zapłaciła za bilety?
A) 20 zł B) 16 zł C) 18 zł D) 15 zł
Dany jest równoległobok 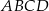 , w którym przekątna
, w którym przekątna 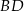 jest prostopadła do boku
jest prostopadła do boku 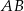 . Kąt ostry tego równoległoboku ma miarę
. Kąt ostry tego równoległoboku ma miarę 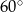 . Długości odcinków
. Długości odcinków 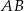 i
i  opisano na rysunku wyrażeniami algebraicznymi.
opisano na rysunku wyrażeniami algebraicznymi.
Obwód równoległoboku 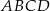 jest równy
jest równy
A) 30 B) 20 C) 15 D) 10
W trójkącie 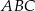 poprowadzono wysokości
poprowadzono wysokości 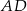 i
i 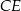 . Odcinek
. Odcinek 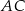 ma taką samą długość
ma taką samą długość  , a kąt
, a kąt  ma miarę
ma miarę  (zobacz rysunek).
(zobacz rysunek).
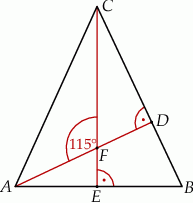
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 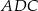 jest równoramienny. jest równoramienny. | P | F |
Kąt 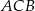 ma miarę ma miarę 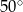 . . | P | F |
Liczba ścian ostrosłupa prawidłowego jest o 5 mniejsza niż liczba jego krawędzi. Pole powierzchni całkowitej tego ostrosłupa jest równe 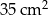 , a pole podstawy jest równe
, a pole podstawy jest równe 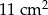 . Pole jednej ściany bocznej tego ostrosłupa jest równe
. Pole jednej ściany bocznej tego ostrosłupa jest równe
A) 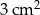 B)
B) 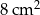 C)
C) 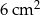 D)
D) 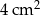
Na dłuższym boku prostokąta zbudowano trójkąt równoboczny o obwodzie 24 cm, a na krótszym boku prostokąta zbudowano kwadrat o polu równym 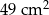 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód prostokąta jest o 6 cm dłuższy od obwodu trójkąta równobocznego zbudowanego na dłuższym boku prostokąta. | P | F |
Pole prostokąta jest o 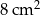 większe od pola kwadratu powstałego na krótszym boku prostokąta. większe od pola kwadratu powstałego na krótszym boku prostokąta. | P | F |
W pudełku było wyłącznie 9 kulek zielonych i 6 kulek niebieskich. Po dołożeniu do tego pudełka pewnej liczby kulek zielonych prawdopodobieństwo wylosowania kulki niebieskiej jest równe 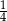 . Ile kulek zielonych dołożono do pudełka?
. Ile kulek zielonych dołożono do pudełka?
A) 10 B) 9 C) 18 D) 6
W jednej szklance o pojemności 250 mililitrów mieści się maksymalnie 150 gramów mąki. Babcia Zosi chce zrobić zapas mąki w pięciolitrowym pojemniku. Czy w takim pojemniku zmieści się 3 kg mąki?
Dany jest romb 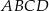 . Obwód tego rombu jest równy 68 cm, a przekątna
. Obwód tego rombu jest równy 68 cm, a przekątna 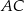 ma długość 30 cm (zobacz rysunek poniżej).
ma długość 30 cm (zobacz rysunek poniżej).
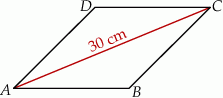
Oblicz długość przekątnej 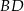 rombu
rombu  .
.
Panczenista potrzebował 5 minut na wykonanie pełnych 10 okrążeń toru łyżwiarskiego o długości 400 m. Z jaką średnią prędkością wyrażoną w 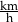 poruszał się ten panczenista?
poruszał się ten panczenista?
Na rysunku przedstawiono siatkę graniastosłupa prostego, którego podstawą jest równoległobok. Na rysunku zapisano niektóre wymiary tej siatki.
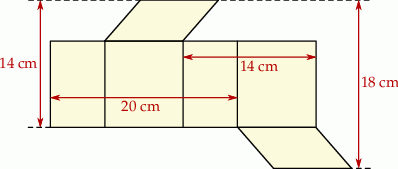
Oblicz objętość tego graniastosłupa.

