/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2023/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 6 maja 2023 Czas pracy: 100 minut
Na diagramie przedstawiono wyniki ankiety, w której uczniowie pewnej szkoły odpowiadali na pytanie „Jakie jest twoje ulubione zwierzę domowe?”. Każdy ankietowany uczeń podawał tylko jedno zwierzę. Psa wskazało o 15 uczniów więcej niż chomika, a kota wskazało 6 razy więcej uczniów niż królika.
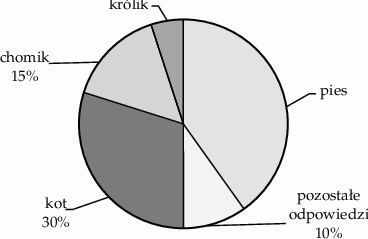
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Królika wskazało A/B uczniów.
A) 3 B) 5
Psa wskazało o C/D uczniów więcej niż kota.
C) 8 D) 6
Wartość wyrażenia 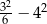 jest równa
jest równa
A) 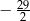 B)
B) 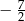 C)
C)  D)
D) 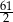
Dane są liczby: 1645, 3376, 1734, 7182, 2948, 2472.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wśród danych liczb są dokładnie A/B liczby podzielne przez 3.
A) trzy B) cztery
Wśród danych liczb są dokładnie C/D liczby podzielne przez 4.
C) dwie D) trzy
Wartość wyrażenia algebraicznego
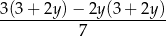
obliczono dla pięciu różnych wartości 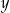 :
:
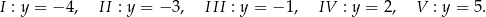
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Największą wartość wyrażenia otrzymano w przypadku A/B .
A) I B) III
Najmniejszą wartość wyrażenia otrzymano w przypadku C/D .
C) II D) V
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 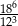 jest równa A/B .
jest równa A/B .
A) 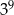 B)
B) 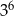
Wartość wyrażenia 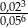 jest równa C/D .
jest równa C/D .
C) 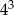 D)
D) 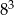
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 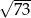 jest
jest
A) większa od 3 i mniejsza od 4. B) większa od 4 i mniejsza od 5.
C) większa od 7 i mniejsza od 8. D) większa od 8 i mniejsza od 9.
Różnica dwóch dodatnich liczb  i
i 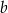 jest równa 76. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest równa 76. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po zmniejszeniu każdej z tych liczb o 6 różnica otrzymanych liczb będzie równa 64. | P | F |
| Po zwiększeniu każdej z tych liczb o połowę różnica otrzymanych liczb będzie równa 114. | P | F |
Na osi liczbowej zaznaczono punkty 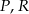 i
i 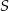 oraz podano współrzędne punktów
oraz podano współrzędne punktów 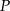 i
i 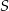 . Punkt
. Punkt 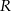 dzieli odcinek
dzieli odcinek 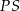 w taki sposób, że stosunek długości odcinków
w taki sposób, że stosunek długości odcinków 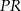 i
i 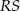 jest równy
jest równy 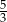 .
.
![]()
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Współrzędna punktu 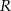 jest równa
jest równa
A) 21 B) 18 C) 16 D) 24
Każdy z dwóch pojemników był początkowo wypełniony 1 kg wodnego roztworu soli o stężeniu 5%. Do pierwszego pojemnika dosypano 150 g soli i dolano 1,55 kg wody. Do drugiego pojemnika dosypano 100 g soli i dolano 0,925 kg wody. Czy stężenie roztworu soli w pojemniku I jest większe niż w pojemniku II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | stężenia soli w obu pojemnikach są takie same. |
| B) | 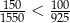 . . |
| C) | 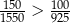 . . |
Plik z prezentacją multimedialną Leszka ma rozmiar 19 MB (megabajtów). Plik z prezentacją multimedialną Izy ma 1,5 razy większy rozmiar (wyrażony w MB) niż plik z prezentacją Leszka.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Plik z prezentacją Leszka ma mniejszy rozmiar niż plik z prezentacją Izy o
A) 12 MB B) 8,5 MB C) 11 MB D) 9,5 MB
W pudełku znajdowały się piłeczki niebieskie i czerwone – łącznie 96. Wśród wszystkich piłeczek 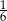 stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi
stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi
A) 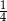 B)
B) 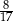 C)
C) 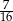 D)
D) 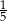
Ogrodnik kupił ziemię ogrodową, którą zaplanował zużyć w maju, czerwcu i lipcu. W maju zużył  masy kupionej ziemi. W czerwcu zużył
masy kupionej ziemi. W czerwcu zużył  masy ziemi, która została. Na lipiec pozostało mu jeszcze 50 kg ziemi.
masy ziemi, która została. Na lipiec pozostało mu jeszcze 50 kg ziemi.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeżeli przez  oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
A) 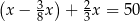 B)
B) 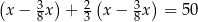
C) 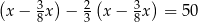 D)
D) 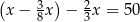
W trapezie 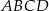 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 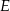 . Pole trójkąta
. Pole trójkąta 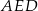 jest równe
jest równe 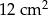 , a pole trójkąta
, a pole trójkąta 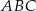 jest równe
jest równe 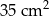 .
.
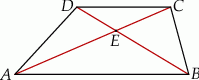
Pole trójkąta 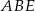 jest równe
jest równe
A) 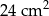 B)
B) 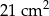 C)
C) 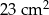 D)
D) 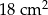
Na rysunku przedstawiono trapez 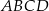 zbudowany z dwóch równoramiennych trójkątów prostokątnych. Krótsza przekątna tego trapezu ma długość 10 cm.
zbudowany z dwóch równoramiennych trójkątów prostokątnych. Krótsza przekątna tego trapezu ma długość 10 cm.
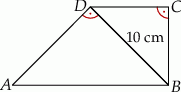
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trapezu 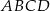 jest równy jest równy 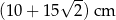 . . | P | F |
Pole trapezu 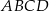 jest równe jest równe 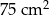 . . | P | F |
Na rysunku przedstawiono siatkę graniastosłupa prostego oraz podano długości niektórych jego krawędzi.
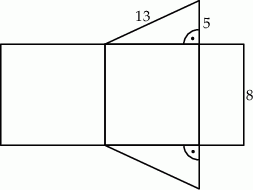
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole największej ściany bocznej tego graniastosłupa jest równe 96. | P | F |
| Pole podstawy tego graniastosłupa jest równe 30. | P | F |
Rowerzysta przejechał ze stałą prędkością trasę o długości 10,5 km od godziny 13:43 do godziny 14:18. Oblicz prędkość, z jaką rowerzysta przejechał tę trasę. Wynik wyraź w 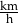 .
.
W trzech salach lekcyjnych było początkowo 44 uczniów. Gdy z trzeciej sali 2 uczniów przeszło do pierwszej sali, a z pierwszej sali 6 uczniów przeszło do drugiej sali to okazało się, że w drugiej sali jest dwa razy więcej uczniów niż w pierwszej sali oraz trzy razy więcej uczniów niż w trzeciej sali. Ilu uczniów było początkowo w trzeciej sali?
W pojemniku znajduje się 60 kolorowych klocków o jednakowym kształcie. Wśród tych klocków jest 25 klocków czerwonych i 17 niebieskich. Pozostałe klocki są zielone. Ania, nie zaglądając do pudełka, wyjmuje z niego kolejno po jednym klocku. Ile co najmniej klocków musi wyjąć Ania, żeby mieć pewność, że wśród wyjętych klocków są co najmniej 3 niebieskie?
Równoległobok 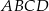 zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości
zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości 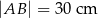 i
i 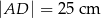 .
.
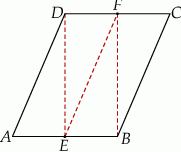
Oblicz pole równoległoboku  .
.

