/Szkoła średnia/Zadania maturalne/Matura 2023/Matura
Egzamin Maturalny
z Matematyki (termin dodatkowy)
formuła 2015
poziom rozszerzony 2 czerwca 2023 Czas pracy: 180 minut
Zadania zamknięte
Wartość wyrażenia 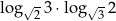 jest równa
jest równa
A)  B)
B) 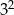 C)
C) 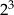 D) 4
D) 4
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 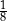 B)
B) 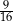 C)
C)  D)
D) 
Reszta z dzielenia wielomianu 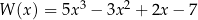 przez dwumian
przez dwumian 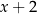 jest równa
jest równa
A) 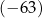 B)
B) 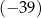 C) 25 D) 41
C) 25 D) 41
Funkcja 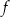 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Fragment wykresu funkcji
. Fragment wykresu funkcji 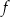 przedstawiono na poniższym rysunku.
przedstawiono na poniższym rysunku.
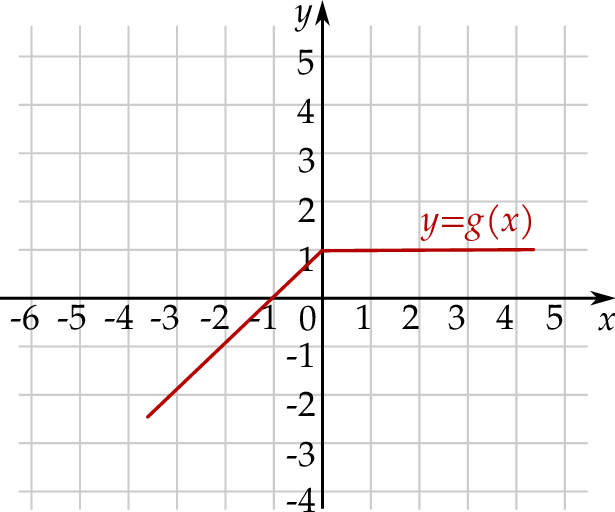
Funkcja 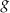 jest określona wzorem
jest określona wzorem 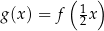 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wskaż rysunek, na którym przedstawiony jest wykres funkcji
. Wskaż rysunek, na którym przedstawiony jest wykres funkcji 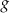 .
.
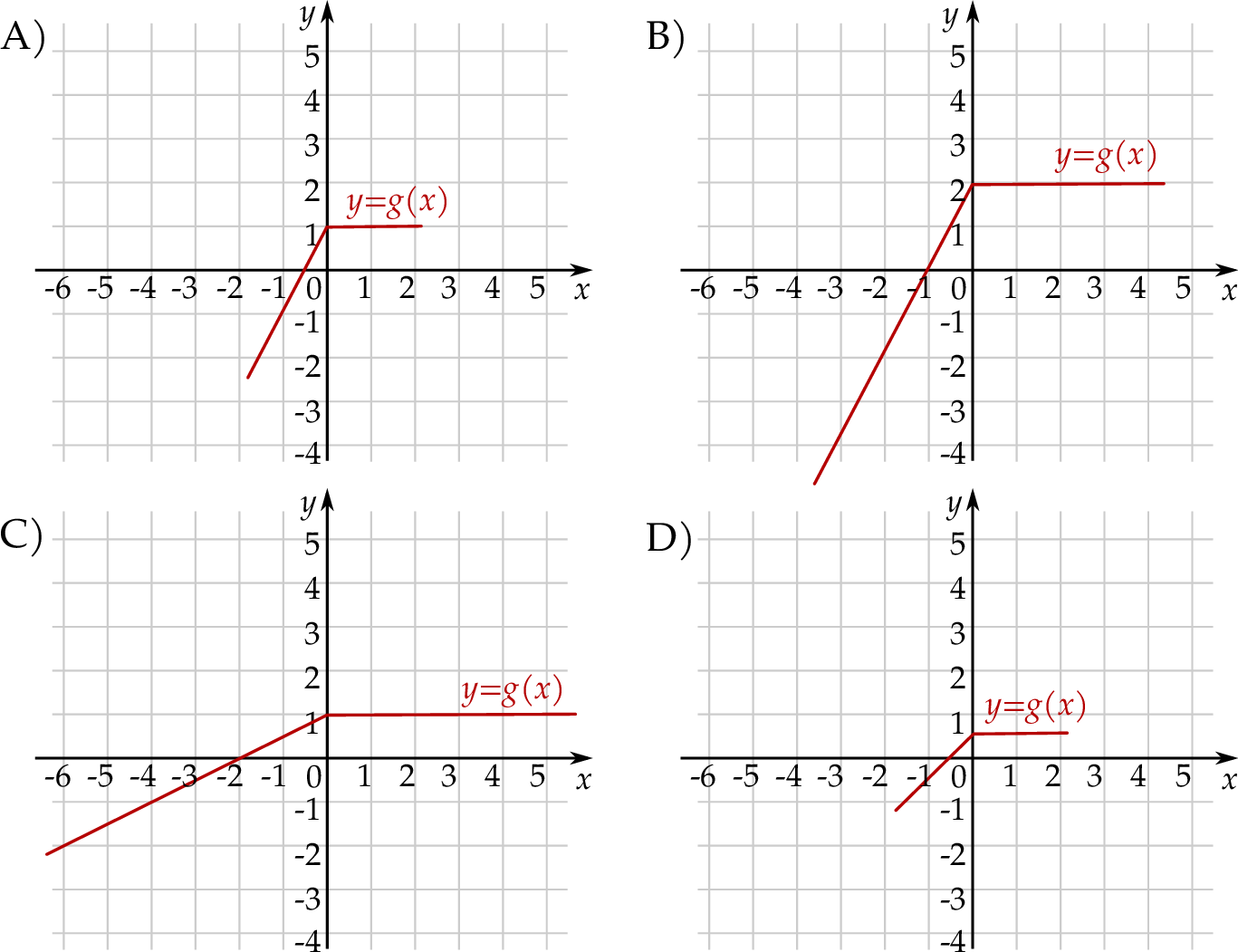
Zadania otwarte
Oblicz granicę
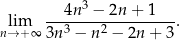
Funkcja 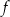 jest określona wzorem
jest określona wzorem 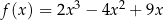 dla każdego
dla każdego 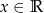 . Punkt
. Punkt 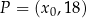 należy do wykresu funkcji
należy do wykresu funkcji 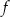 . Oblicz
. Oblicz 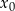 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 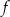 w punkcie
w punkcie 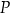 .
.
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
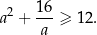
Dany jest okrąg 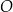 . Przez punkt
. Przez punkt 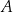 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 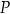 oraz
oraz 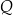 . Przez punkt
. Przez punkt 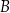 leżący na odcinku
leżący na odcinku 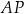 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 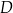 , która przecięła odcinek
, która przecięła odcinek 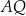 w punkcie
w punkcie 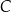 (zobacz rysunek).
(zobacz rysunek).
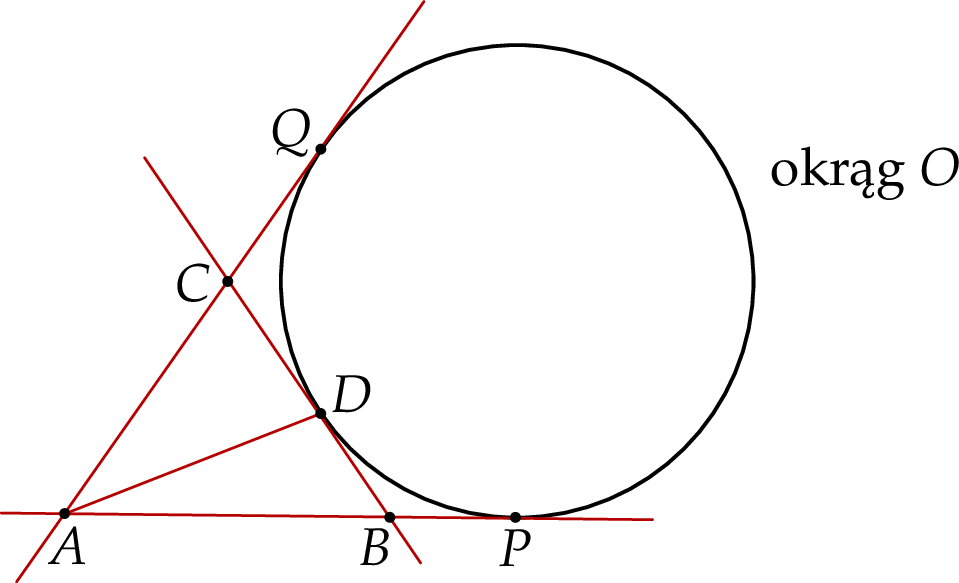
Wykaż, że jeżeli 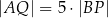 oraz
oraz 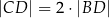 , to trójkąt
, to trójkąt 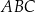 jest równoramienny.
jest równoramienny.
Dany jest nieskończony szereg geometryczny
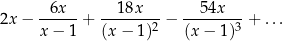
Wyznacz wszystkie wartości zmiennej  (różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest równa
(różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest równa 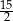 .
.
Rozwiąż równanie 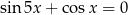 w zbiorze
w zbiorze ![[− π-, π] 2 2](https://img.zadania.info/zes/0043965/HzesT49x.png) .
.
W pudełku umieszczono  kul (
kul (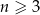 ) wśród których dokładnie 2 kule są czarne, a pozostałe kule są białe. Z tego pudełka losujemy jedną kulę i odkładamy ją na bok. Jeżeli wylosowana kula jest biała, to do pudełka wrzucamy kulę czarną, a gdy wylosowana kula jest czarna, to do pudełka wrzucamy kulę białą. Po przeprowadzonej w ten sposób zmianie zawartości prawdopodobieństwo wylosowania kuli białej z tego pudełka jest równe
) wśród których dokładnie 2 kule są czarne, a pozostałe kule są białe. Z tego pudełka losujemy jedną kulę i odkładamy ją na bok. Jeżeli wylosowana kula jest biała, to do pudełka wrzucamy kulę czarną, a gdy wylosowana kula jest czarna, to do pudełka wrzucamy kulę białą. Po przeprowadzonej w ten sposób zmianie zawartości prawdopodobieństwo wylosowania kuli białej z tego pudełka jest równe 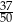 . Oblicz
. Oblicz  .
.
Wyznacz wszystkie wartości parametru 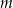 , dla których równanie
, dla których równanie
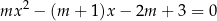
ma dokładnie dwa różne rozwiązania rzeczywiste 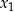 oraz
oraz 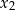 , spełniające warunki:
, spełniające warunki:
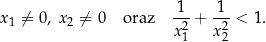
Czworokąt wypukły 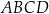 jest wpisany w okrąg o promieniu 4. Kąty
jest wpisany w okrąg o promieniu 4. Kąty 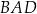 i
i 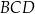 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 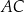 i
i 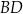 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 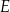 tak, że
tak, że 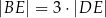 oraz
oraz 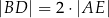 .
.

Oblicz długości boków czworokąta 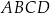 .
.
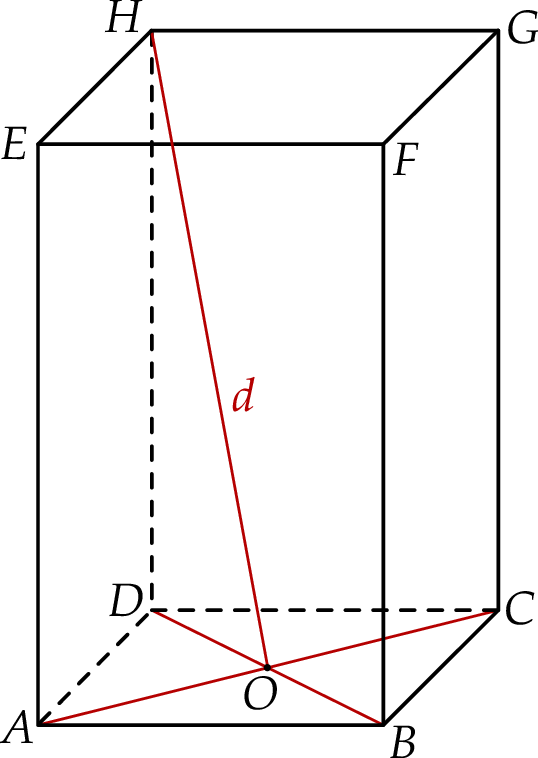
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne 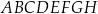 , w których odcinek łączący punkt
, w których odcinek łączący punkt 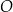 przecięcia przekątnych
przecięcia przekątnych 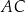 i
i 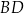 podstawy
podstawy 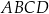 z dowolnym wierzchołkiem podstawy
z dowolnym wierzchołkiem podstawy 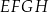 ma długość
ma długość 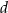 (zobacz rysunek).
(zobacz rysunek).
-
Wyznacz zależność objętości
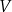 graniastosłupa od jego wysokości
graniastosłupa od jego wysokości 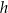 i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 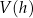 .
. -
Wyznacz wysokość tego z rozważanych graniastosłupów, którego objętość jest największa.
Okrąg 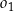 o środku w punkcie
o środku w punkcie 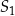 jest określony równaniem
jest określony równaniem 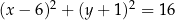 . Okrąg
. Okrąg 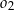 ma środek w punkcie
ma środek w punkcie 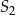 takim, że
takim, że ![−→ S1S2 = [− 4,4]](https://img.zadania.info/zes/0043965/HzesT85x.png) . Promienie tych okręgów są sobie równe. Figura
. Promienie tych okręgów są sobie równe. Figura 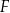 składa się z dwóch okręgów:
składa się z dwóch okręgów: 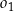 oraz
oraz 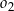 . Punkty
. Punkty 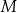 i
i 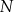 są punktami przecięcia figury
są punktami przecięcia figury 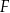 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt
z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 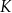 , leżący na jednej z osi symetrii figury
, leżący na jednej z osi symetrii figury 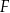 , taki, że pole trójkąta
, taki, że pole trójkąta 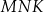 jest równe 40.
jest równe 40.

