/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Pole

Zadanie nr 3816623

Na czworokącie wypukłym 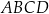ABCD można opisać okrąg. Wiadomo, że 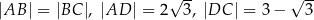√ -- √ -- |AB | = |BC |, |AD | = 2 3, |DC | = 3− 3 oraz przekątna 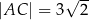√ -- |AC | = 3 2 . Oblicz pole tego czworokąta.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

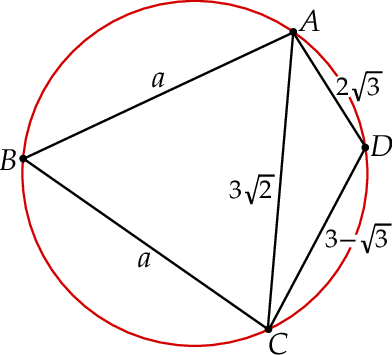
Zauważmy, że podane długości boków trójkąta 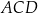ACD pozwalają obliczyć cosinus kąta 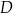D . Aby to zrobić piszemy twierdzenie cosinusów.

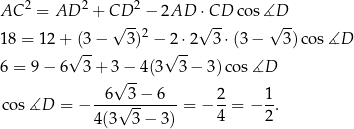
AC 2 = AD 2 + CD 2 − 2AD ⋅CD cos ∡D √ --2 √ -- √ -- 18 = 12 +√(3-− 3) −√2-⋅2 3⋅ (3− 3)cos ∡D 6 = 9− 6 3 + 3 − 4(3 3 − 3) cos∡D √ -- -6--3-−-6--- 2- 1- cos ∡D = − 4(3√ 3− 3) = − 4 = − 2.

To oznacza, że 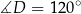∘ ∡D = 120 . Możemy teraz obliczyć pole trójkąta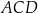 ACD

1 1 √ -- √ -- √ 3- PACD = --⋅AD ⋅CD sin12 0∘ = --⋅2 3 ⋅(3 − 3) ⋅----= 2 √ -- 2 2 9−--3--3- = 2 .

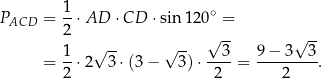
Patrzymy teraz na trójkąt 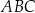ABC . Jest to trójkąt równoramienny, oraz

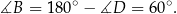
∡B = 180 ∘ − ∡D = 60 ∘.

Jest to więc trójkąt równoboczny o boku długości 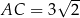√ -- AC = 3 2 . Liczymy jego pole

2√ -- √ -- √ -- PABC = a---3-= 18--3-= 9--3. 4 4 2

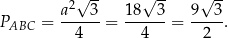
Pole czworokąta 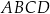ABCD jest więc równe

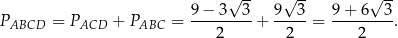
√ -- √ -- √ -- PABCD = PACD + PABC = 9−--3--3-+ 9---3 = 9-+-6--3-. 2 2 2

 
Odpowiedź: √- 9+-62-3

Wersja PDF