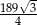/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Pole

Zadanie nr 3949675

W okrąg o promieniu 7 wpisano czworokąt 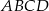ABCD . Oblicz obwód i pole tego czworokąta, wiedząc, że 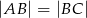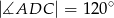|AB | = |BC | , |∡ADC | = 120∘ i stosunek pola trójkąta 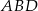ABD do pola trójkąta 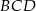BCD wynosi 2:1.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

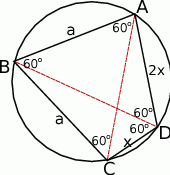
Ponieważ suma przeciwległych kątów czworokąta wpisanego w okrąg wynosi 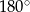180 ∘ , więc

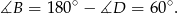
∡B = 180 ∘ − ∡D = 60 ∘.

Ale w takiej sytuacji trójkąt 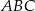ABC musi być równoboczny (bo jest równoramienny, więc pozostałe jego kąty też są równe 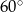60∘ ). Od razu obliczmy długość a jego boku. Promień okręgu opisanego na trójkącie równobocznym to 2 3 jego wysokości, czyli

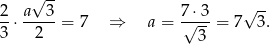
√ -- √ -- 2⋅ a--3-= 7 ⇒ a = 7√⋅3-= 7 3. 3 2 3

Zatem pole tego trójkąta jest równe

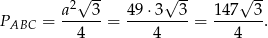
√ -- √ -- √ -- a2--3- 49-⋅3--3- 147--3- PABC = 4 = 4 = 4 .

Ok, teraz pora zabrać się za trójkąt 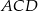ACD . Zauważmy, że

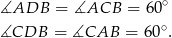
∘ ∡ADB = ∡ACB = 60 ∡CDB = ∡CAB = 60∘.

Zatem podany warunek o stosuku pól możemy zapisać w postaci

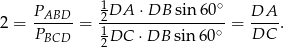
PABD-- 12DA---⋅DB--sin-60∘- DA-- 2 = P = 1DC ⋅ DB sin 60∘ = DC . BCD 2

Oznaczmy 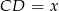CD = x – długość tego odcinka możemy wyliczyć z twierdzenia cosinusów w trójkącie CDA .

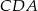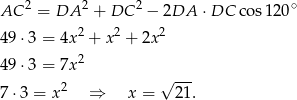
2 2 2 ∘ AC = DA + DC − 2DA ⋅DC co s120 49⋅ 3 = 4x2 + x2 + 2x2 49⋅ 3 = 7x2 2 √ --- 7⋅3 = x ⇒ x = 21.

Możemy teraz wyliczyć obwód czworokąta 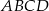ABCD :

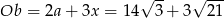
√ -- √ --- Ob = 2a + 3x = 1 4 3+ 3 21

Pozostało policzyć pole trójkąta 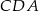CDA .

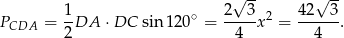
√ -- √ -- P = 1-DA ⋅DC sin 120 ∘ = 2--3-x2 = 42---3. CDA 2 4 4

Zatem pole czworokąta jest równe

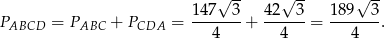
√ -- √ -- √ -- PABCD = PABC + PCDA = 147--3-+ 42--3-= 189--3-. 4 4 4

 
Odpowiedź: Obwód: 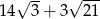√ -- √ --- 14 3 + 3 21 , pole: √ - 189--3 4

Wersja PDF