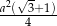/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Pole

Zadanie nr 5123280

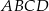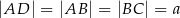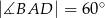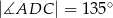Dany jest czworokąt wypukły ABCD , w którym |AD | = |AB | = |BC | = a , |∡BAD | = 60∘ i |∡ADC | = 135∘ . Oblicz pole czworokąta ABCD .

Wersja PDF

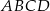Rozwiązanie

Jak zwykle, zacznijmy od schematycznego rysunku.

PIC

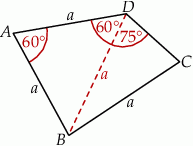
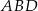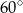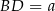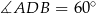Zauważmy, że trójkąt ABD jest równoramienny z kątem między ramionami równym 6 0∘ , więc jest to trójkąt równoboczny. W szczególności BD = a i ∡ADB = 6 0∘ . To oznacza, że trójkąt 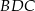BDC jest równoramienny i

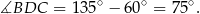
∡BDC = 135 ∘ − 60 ∘ = 75∘.

Stąd

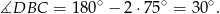
∡DBC = 180∘ − 2 ⋅75∘ = 30 ∘.

Teraz już łatwo obliczyć pole czworokąta ABCD .

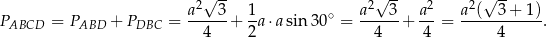
√ -- √ -- √ -- a2 3 1 ∘ a 2 3 a2 a 2( 3 + 1 ) PABCD = PABD + PDBC = --4---+ 2a ⋅asin 30 = ---4--+ 4--= -----4------.

 
Odpowiedź: 2 √- a-(-34+-1)

Wersja PDF