/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Pole

Zadanie nr 5599713

Na czworokącie wypukłym 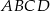ABCD , w którym 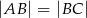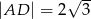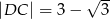|AB | = |BC | , √ -- |AD | = 2 3 , √ -- |DC | = 3 − 3 można opisać okrąg. Wiedząc, że przekątna 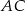AC ma długość 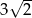√ -- 3 2 , oblicz pole tego czworokąta.

Wersja PDF

Rozwiązanie

Jak zwykle zaczynamy od schematycznego rysunku.

PIC

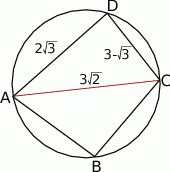
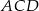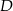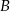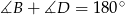Plan jest następujący: ponieważ znamy wszystkie boki trójkąta ACD , możemy wyliczyć jego kąt przy wierzchołku D (z twierdzenia cosinusów), to nam da kąt B (bo ∡B + ∡D = 180∘ ), a to z kolei powinno pozwolić wyliczyć długość boku 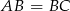AB = BC (znowu z twierdzenia cosinusów).

No to liczymy

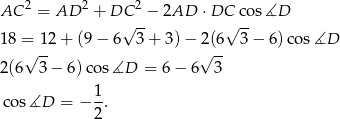
2 2 2 AC = AD + DC√ --− 2AD ⋅DC√ co-s∡D 18 = 12 + (9 − 6 3 + 3) − 2(6 3− 6 )cos ∡D √ -- √ -- 2(6 3 − 6)co s∡D = 6− 6 3 1 cos ∡D = − -. 2

A zatem 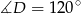∘ ∡D = 120 , skąd 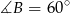∘ ∡B = 60 . Ponieważ 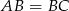AB = BC , oznacza to, że trójkąt 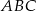ABC jest równoboczny. Możemy teraz policzyć szukane pole

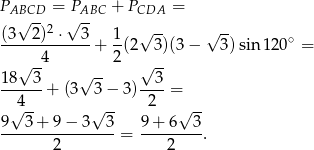
PABCD-- = PABC + PCDA = (3√ 2)2 ⋅ √ 3 1 √ -- √ -- ------------+ -(2 3)(3− 3)sin1 20∘ = √ -4 2 √ -- 18--3- √ -- --3- 4 + (3 3 − 3) 2 = √ -- √ -- √ -- 9--3+--9−--3--3-= 9+--6--3. 2 2

 
Odpowiedź: √- 9+-62-3

Wersja PDF