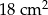Zadanie nr 9855782
Z punktu 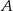 leżącego na okręgu o promieniu
leżącego na okręgu o promieniu 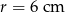 i środku
i środku  poprowadzono dwie równej długości cięciwy
poprowadzono dwie równej długości cięciwy 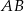 i
i 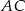 tworzące kąt
tworzące kąt 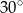 . Oblicz pole czworokąta
. Oblicz pole czworokąta 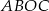 .
.
Rozwiązanie
Zaczynamy od rysunku.
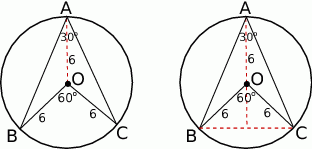
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, mamy
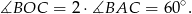
Sposób I
Jeżeli połączymy środek 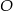 okręgu z punktem
okręgu z punktem 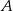 to mamy dwa przystające trójkąty równoramienne
to mamy dwa przystające trójkąty równoramienne 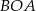 i
i 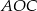 o ramionach długości
o ramionach długości 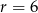 . Kąt między ramionami wynosi
. Kąt między ramionami wynosi 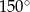 , zatem pole jednego takiego trójkąta jest równe
, zatem pole jednego takiego trójkąta jest równe
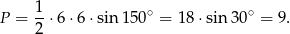
Pole całego czworokąta jest dwa razy większe.
Sposób II
Zadanie możemy też rozwiązać bez trygonometrii. Obliczymy szukane pole czworokąta odejmując od pola trójkąta 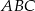 pole trójkąta
pole trójkąta 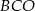 .
.
Trójkąt 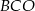 jest równoboczny (bo jest równoramienny i jeden z jego kątów ma miarę
jest równoboczny (bo jest równoramienny i jeden z jego kątów ma miarę 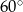 ). Zatem jego pole jest równe
). Zatem jego pole jest równe
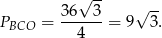
Zauważmy ponadto, że wysokość 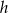 trójkąta
trójkąta 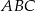 opuszczona na podstawę
opuszczona na podstawę 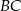 jest sumą promienia okręgu i wysokości trójkąta
jest sumą promienia okręgu i wysokości trójkąta 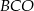 . Zatem
. Zatem
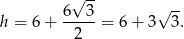
Zatem pole trójkąta 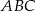 jest równe
jest równe
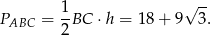
Stąd
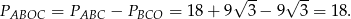
Odpowiedź: