Zadanie nr 5342225
Punkt 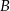 jest obrazem punktu
jest obrazem punktu 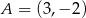 w symetrii względem początku układu współrzędnych, a punkt
w symetrii względem początku układu współrzędnych, a punkt 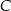 jest obrazem punktu
jest obrazem punktu 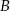 w symetrii względem punktu
w symetrii względem punktu 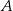 . Długość odcinka
. Długość odcinka 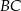 jest równa
jest równa
A) 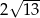 B)
B) 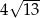 C)
C) 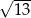 D)
D) 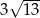
Rozwiązanie
Szkicujemy opisaną sytuację.
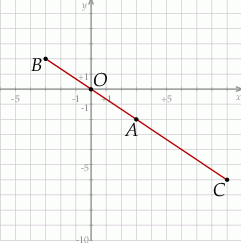
Sposób I
Z rysunku powinno być jasne, że
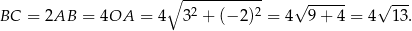
Sposób II
Z rysunku powinno być jasne, że 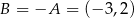 . Ponadto
. Ponadto 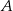 jest środkiem odcinka
jest środkiem odcinka 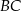 , więc
, więc
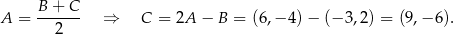
Zatem
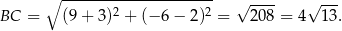
Odpowiedź: B

