/Szkoła średnia/Zadania maturalne/Matura 2024

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 6 kwietnia 2024 Czas pracy: 180 minut

Zadanie 1

(2 pkt)

W chwili początkowej 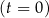(t = 0) masa substancji jest równa 12 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 21% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej 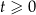t ≥ 0 funkcja 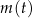m (t) określa masę substancji w gramach po 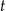pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji 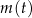m (t) . Oblicz, przez ile pełnych dób masa tej substancji będzie przekraczać 3 gramy.

Zadanie 2

(3 pkt)

Wykaż, że dla dowolnych dodatnich liczb rzeczywistych i 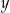prawdziwa jest nierówność

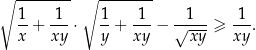
∘ -------- ∘ -------- 1-+ -1-⋅ 1-+ 1--− √-1-- ≥ -1-. x xy y xy xy xy

Zadanie 3

(3 pkt)

Ciąg 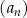(an) jest określony wzorem

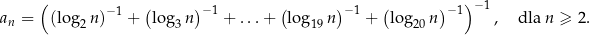
( ( ) ( ) ( ) )− 1 an = (lo g n)− 1 + lo g n −1 + ...+ log n − 1 + log n − 1 , dla n ≥ 2. 2 3 19 20

Oblicz sumę 19 początkowych wyrazów ciągu 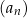(an) .

Zadanie 4

(3 pkt)

Funkcja 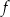jest określona wzorem 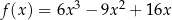f(x ) = 6x3 − 9x2 + 16x dla każdego 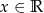x ∈ R . Punkt 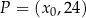P = (x0,24) należy do wykresu funkcji 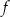. Oblicz 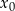oraz wyznacz równanie stycznej do wykresu funkcji 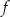w punkcie .

Zadanie 5

(4 pkt)

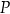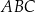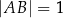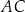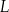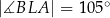Dany jest trójkąt równoboczny ABC , w którym |AB | = 1 . Na boku tego trójkąta wybrano taki punkt , że ∘ |∡BLA | = 105 . Odcinek 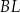przecina wysokość 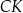trójkąta 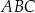ABC w punkcie 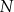(zobacz rysunek).

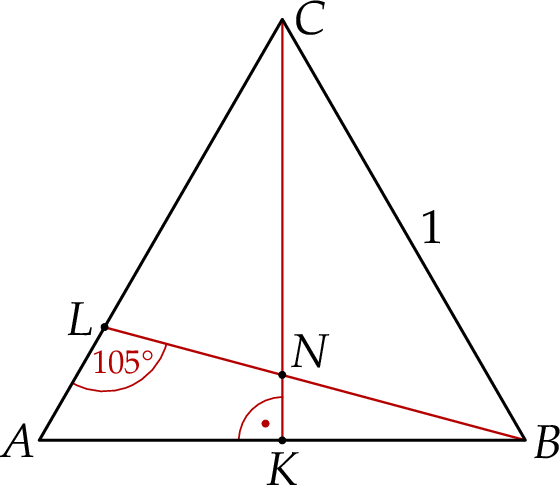
ZINFO-FIGURE

Oblicz długość odcinka .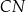

Zadanie 6

(3 pkt)

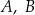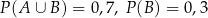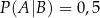O zdarzeniach losowych A , B wiadomo, że: P(A ∪ B) = 0 ,7, P (B) = 0 ,3 i P(A |B) = 0,5 . Oblicz prawdopodobieństwo warunkowe P(B |A) .

Zadanie 7

(4 pkt)

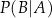Dany jest nieskończony szereg geometryczny

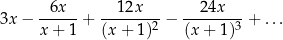
3x − -6x---+ ---12x---− --24x---+ ... x + 1 (x + 1 )2 (x+ 1)3

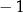Wyznacz wszystkie wartości zmiennej (różnej od − 1 i od 0), dla których suma tego szeregu istnieje i jest równa 187 2 .

Zadanie 8

(4 pkt)

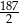Rozwiąż równanie

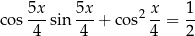
cos 5x-sin 5x-+ co s2 x-= 1 4 4 4 2

w zbiorze [− π ,π] .

Zadanie 9

(4 pkt)

Rozwiąż nierówność 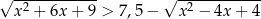√ ------------ √ ------------ x 2 + 6x + 9 > 7,5 − x2 − 4x + 4 .

Zadanie 10

(4 pkt)

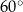Każda ściana graniastosłupa jest rombem o boku długości i kącie ostrym o mierze ∘ 6 0 . Oblicz objętość tego graniastosłupa.

Zadanie 11

(5 pkt)

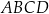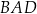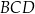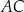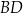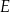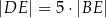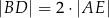Czworokąt wypukły ABCD jest wpisany w okrąg o promieniu 9. Kąty BAD i BCD są proste (zobacz rysunek). Przekątne i tego czworokąta przecinają się w punkcie tak, że |DE | = 5 ⋅|BE | oraz |BD | = 2⋅ |AE | .

ZINFO-FIGURE

Oblicz długości boków czworokąta 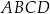ABCD .

Zadanie 12

(5 pkt)

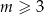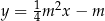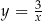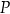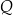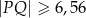Dla dowolnej liczby m ≥ 3 , prosta 1 2 y = 4m x − m przecina hiperbolę 3 y = x w punktach i . Uzasadnij, że |P Q| ≥ 6,56 .

Zadanie 13

(6 pkt)

Czworokąt 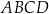ABCD jest wpisany w okrąg o środku 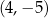(4,− 5) i promieniu 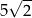√ -- 5 2 . Przekątna 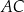zawiera się w prostej o równaniu 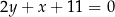2y+ x+ 11 = 0 i tworzy z bokiem 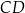kąt o mierze 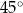∘ 45 . Obie współrzędne punktu 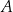są ujemne, a obie współrzędne punktu 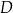są dodatnie. Przekątne czworokąta 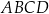ABCD są prostopadłe. Oblicz współrzędne punktu .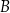