/Szkoła średnia/Zadania maturalne/Matura 2024
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 16 marca 2024 Czas pracy: 180 minut
Jacek ustawia  książek na półce. Wśród tych książek są dokładnie 3 książki historyczne. Liczba wszystkich możliwych ustawień tych książek jest 117 razy większa od liczby wszystkich takich ustawień, w których książki historyczne stoją obok siebie (w dowolnej kolejności). Oblicz
książek na półce. Wśród tych książek są dokładnie 3 książki historyczne. Liczba wszystkich możliwych ustawień tych książek jest 117 razy większa od liczby wszystkich takich ustawień, w których książki historyczne stoją obok siebie (w dowolnej kolejności). Oblicz  .
.
Informacja do zadań 2.1 i 2.2
Dany jest wielomian 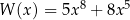 określony dla dowolnej liczby rzeczywistej
określony dla dowolnej liczby rzeczywistej  .
.
Wykaż, równanie 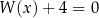 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Wyznacz wszystkie wartości parametru 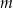 , dla których równanie
, dla których równanie
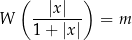
ma przynajmniej jedno rozwiązanie rzeczywiste.
Wykaż, że
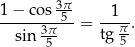
Funkcja 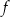 jest określona wzorem
jest określona wzorem 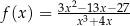 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 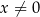 . Prosta
. Prosta 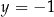 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 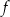 w punkcie
w punkcie 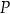 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 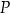 .
.
Okrąg wpisany w trójkąt 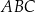 jest styczny do boków
jest styczny do boków 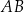 i
i 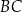 w punktach
w punktach 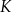 i
i 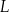 odpowiednio. Na bokach
odpowiednio. Na bokach 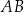 i
i 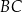 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 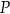 i
i 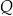 w ten sposób, że odcinek
w ten sposób, że odcinek 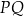 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 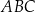 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 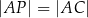 ,
, 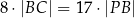 i
i 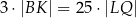 , to trójkąt
, to trójkąt 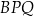 jest rozwartokątny.
jest rozwartokątny.
Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta jest równy 33, a cosinus największego kąta jest równy 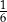 . Oblicz promień okręgu opisanego na tym trójkącie.
. Oblicz promień okręgu opisanego na tym trójkącie.
Dany jest sześcian 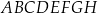 o krawędzi długości 3. Punkt
o krawędzi długości 3. Punkt 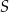 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 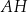 i
i 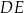 ściany bocznej
ściany bocznej 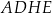 (zobacz rysunek).
(zobacz rysunek).
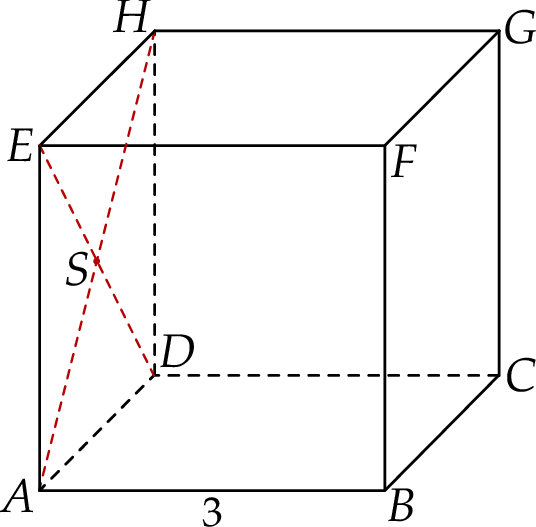
Oblicz wysokość trójkąta 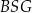 poprowadzoną z punktu
poprowadzoną z punktu 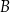 na bok
na bok  tego trójkąta.
tego trójkąta.
Ośmiokrotnie rzucamy sześcienną kostką do gry. Wśród otrzymanych wyników jest dokładnie 5 piątek. Jakie jest prawdopodobieństwo, że w ostatnim rzucie otrzymaliśmy piątkę?
Ciąg 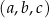 jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
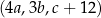
jest trzywyrazowym ciągiem arytmetycznym. Ponadto, spełniony jest warunek 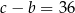 . Oblicz
. Oblicz 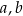 oraz
oraz  .
.
W układzie współrzędnych dane są punkty 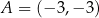 ,
, 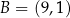 i
i 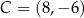 . Wyznacz wszystkie punkty
. Wyznacz wszystkie punkty 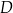 prostej
prostej 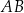 , które są różne od punktów
, które są różne od punktów 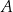 i
i 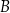 , i dla których suma pól trójkątów
, i dla których suma pól trójkątów 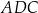 i
i 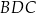 jest mniejsza od 120.
jest mniejsza od 120.
Wyznacz wszystkie wartości parametru 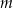 , dla których równanie
, dla których równanie
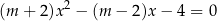
ma dwa różne rozwiązania rzeczywiste 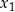 oraz
oraz 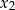 , spełniające warunek:
, spełniające warunek:
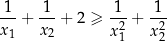
Boki 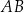 i
i 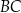 prostokąta
prostokąta 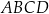 mają długości
mają długości 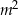 i
i 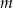 odpowiednio, gdzie
odpowiednio, gdzie 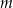 jest ustaloną dodatnią liczbą rzeczywistą. Na bokach
jest ustaloną dodatnią liczbą rzeczywistą. Na bokach 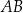 i
i 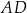 wybrano odpowiednio punkty
wybrano odpowiednio punkty 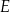 i
i 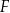 w ten sposób, że
w ten sposób, że 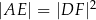 . Oblicz dla jakiej długości odcinka
. Oblicz dla jakiej długości odcinka 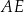 pole trójkąta
pole trójkąta 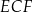 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.

