/Szkoła średnia/Zadania maturalne/Matura 2024
Egzamin Maturalny
z Matematyki poziom podstawowy
(formuła 2015) 8 maja 2024 Czas pracy: 170 minut
Zadania zamknięte
Na początku sezonu letniego cenę  pary sandałów podwyższono o 20%. Po miesiącu nową cenę obniżono o 10%. Po obu tych zmianach ta para sandałów kosztowała 81 zł. Początkowa cena
pary sandałów podwyższono o 20%. Po miesiącu nową cenę obniżono o 10%. Po obu tych zmianach ta para sandałów kosztowała 81 zł. Początkowa cena  pary sandałów była równa
pary sandałów była równa
A) 45 zł B) 73,63 zł C) 75 zł D) 87,48 zł
Liczba 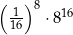 jest równa
jest równa
A) 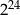 B)
B) 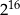 C)
C) 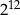 D)
D) 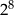
Liczba 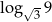 jest równa
jest równa
A) 2 B) 3 C) 4 D) 9
Dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 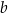 wartość wyrażenia
wartość wyrażenia
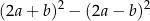
jest równa wartości wyrażenia
A) 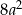 B)
B) 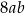 C)
C) 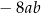 D)
D) 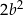
Zbiorem wszystkich rozwiązań nierówności
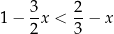
jest przedział
A) 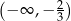 B)
B) 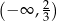 C)
C) 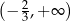 D)
D) 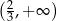
Największą liczbą będącą rozwiązaniem rzeczywistym równania 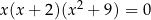 jest
jest
A) 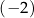 B) 0 C) 2 D) 3
B) 0 C) 2 D) 3
Równanie 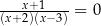 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie: 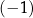 .
.
C) ma dokładnie dwa rozwiązania: 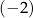 oraz 3.
oraz 3.
D) ma dokładnie trzy rozwiązania: 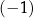 ,
, 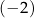 oraz 3.
oraz 3.
W październiku 2022 roku założono dwa sady, w których posadzono łącznie 1960 drzew. Po roku stwierdzono, że uschło 5% drzew w pierwszym sadzie i 10% drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano. Liczba drzew, które pozostały w drugim sadzie, stanowiła 60% liczby drzew, które pozostały w pierwszym sadzie. Niech  oraz
oraz 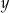 oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby
oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby  drzew posadzonych w pierwszym sadzie oraz liczby
drzew posadzonych w pierwszym sadzie oraz liczby 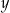 drzew posadzonych w drugim sadzie, jest
drzew posadzonych w drugim sadzie, jest
A) 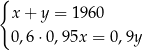 B)
B) 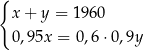
C) 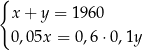 D)
D) 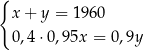
Średnia arytmetyczna trzech liczb: 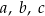 , jest równa 9. Średnia arytmetyczna sześciu liczb:
, jest równa 9. Średnia arytmetyczna sześciu liczb: 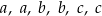 , jest równa
, jest równa
A) 9 B) 6 C) 4,5 D) 18
Na rysunku, w kartezjańskim układzie współrzędnych  , przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
, przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
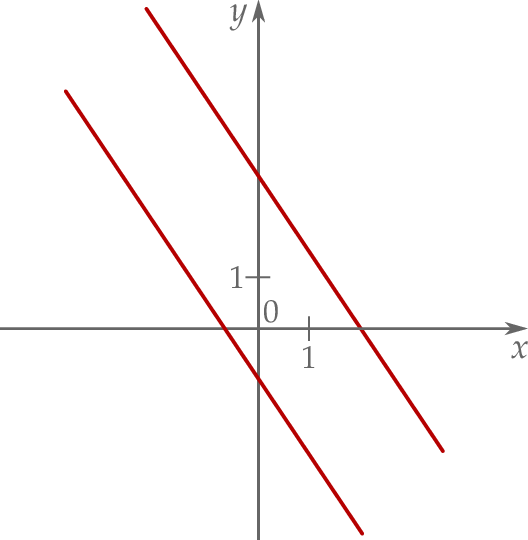
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 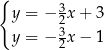 B)
B) 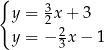
C) 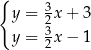 D)
D) 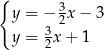
Na rysunku przedstawiono wykres funkcji 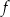 .
.
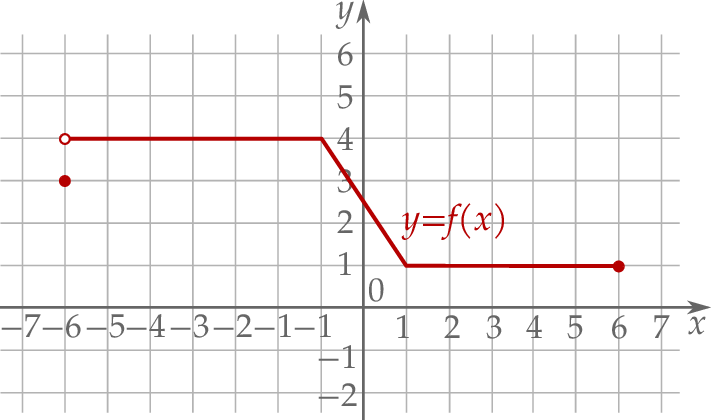
Zbiorem wartości tej funkcji jest
A) ![(− 6,6]](https://img.zadania.info/zes/0081832/HzesT45x.png) B)
B) 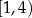 C)
C) ![[1,4]](https://img.zadania.info/zes/0081832/HzesT47x.png) D)
D) ![[− 6,6]](https://img.zadania.info/zes/0081832/HzesT48x.png)
Funkcja liniowa 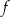 jest określona wzorem
jest określona wzorem 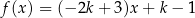 , gdzie
, gdzie 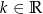 . Funkcja
. Funkcja 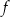 jest malejąca dla każdej liczby
jest malejąca dla każdej liczby 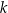 należącej do przedziału
należącej do przedziału
A) 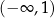 B)
B) 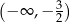 C)
C) 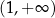 D)
D) 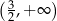
Funkcje liniowe 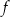 oraz
oraz 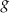 , określone wzorami
, określone wzorami 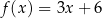 oraz
oraz 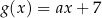 , mają to samo miejsce zerowe. Współczynnik
, mają to samo miejsce zerowe. Współczynnik  we wzorze funkcji
we wzorze funkcji 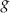 jest równy
jest równy
A) 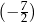 B)
B) 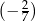 C)
C)  D)
D) 
Informacja do zadań 14 i 15
W kartezjańskim układzie współrzędnych 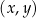 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 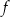 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
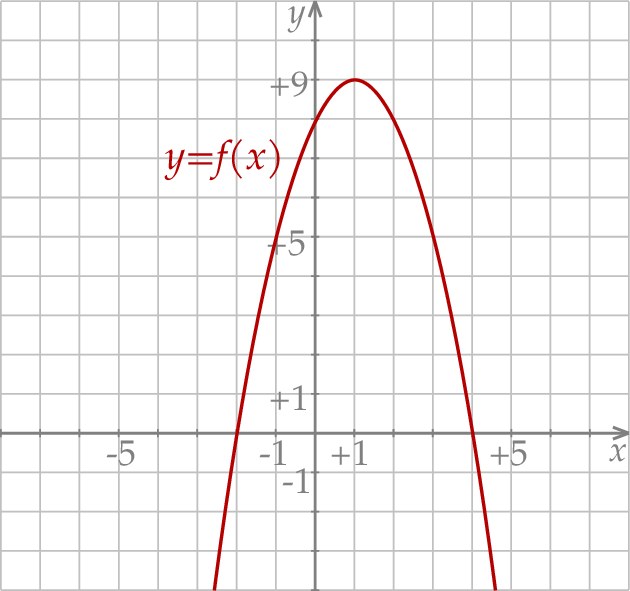
Funkcja kwadratowa 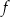 jest określona wzorem
jest określona wzorem
A) 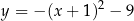 B)
B) 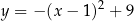
C) 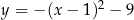 D)
D) 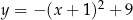
Dla funkcji 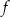 prawdziwa jest równość
prawdziwa jest równość
A) 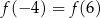 B)
B) 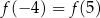 C)
C) 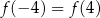 D)
D) 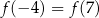
W ciągu arytmetycznym 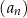 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 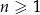 , dane są wyrazy
, dane są wyrazy 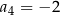 oraz
oraz 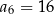 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 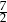 B)
B)  C) 7 D) 9
C) 7 D) 9
Ciąg geometryczny 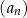 jest określony wzorem
jest określony wzorem 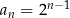 , dla każdej liczby naturalnej
, dla każdej liczby naturalnej 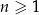 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A)  B)
B) 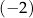 C) 2 D) 1
C) 2 D) 1
Ciąg 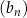 jest określony wzorem
jest określony wzorem 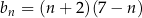 dla każdej liczby naturalnej
dla każdej liczby naturalnej 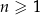 . Liczba dodatnich wyrazów ciągu
. Liczba dodatnich wyrazów ciągu 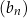 jest równa
jest równa
A) 6 B) 7 C) 8 D) 9
Liczba 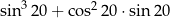 jest równa
jest równa
A) 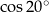 B)
B) 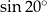 C)
C) 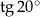 D)
D) 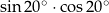
Kąt  jest ostry oraz
jest ostry oraz 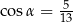 . Wtedy
. Wtedy
A) 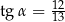 B)
B) 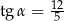 C)
C) 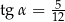 D)
D) 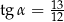
Dany jest równoległobok o bokach długości 3 i 4 oraz o kącie między nimi o mierze 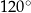 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 12 B) 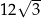 C) 6 D)
C) 6 D) 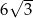
W trójkącie 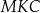 bok
bok 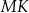 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 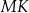 przecina boki
przecina boki 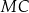 i
i 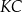 – odpowiednio – w punktach
– odpowiednio – w punktach 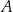 oraz
oraz 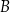 takich, że
takich, że 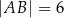 i
i 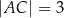 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 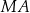 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12
W trójkącie 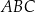 , wpisanym w okrąg o środku w punkcie
, wpisanym w okrąg o środku w punkcie 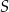 , kąt
, kąt 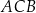 ma miarę
ma miarę 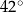 (zobacz rysunek).
(zobacz rysunek).

Miara kąta ostrego 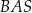 jest równa
jest równa
A) 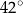 B)
B) 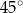 C)
C) 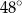 D)
D) 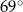
W kartezjańskim układzie współrzędnych 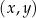 proste
proste 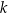 oraz
oraz 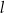 są określone równaniami
są określone równaniami
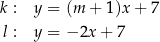
Proste 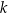 oraz
oraz 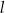 są prostopadłe, gdy liczba
są prostopadłe, gdy liczba 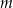 jest równa
jest równa
A) 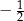 B)
B) 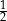 C)
C) 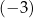 D) 1
D) 1
Na prostej 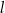 o współczynniku kierunkowym
o współczynniku kierunkowym 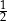 leżą punkty
leżą punkty 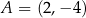 oraz
oraz 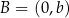 . Wtedy liczba
. Wtedy liczba 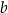 jest równa
jest równa
A) 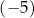 B) 10 C)
B) 10 C) 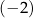 D) 0
D) 0
Wysokość graniastosłupa prawidłowego sześciokątnego jest równa 6 (zobacz rysunek).
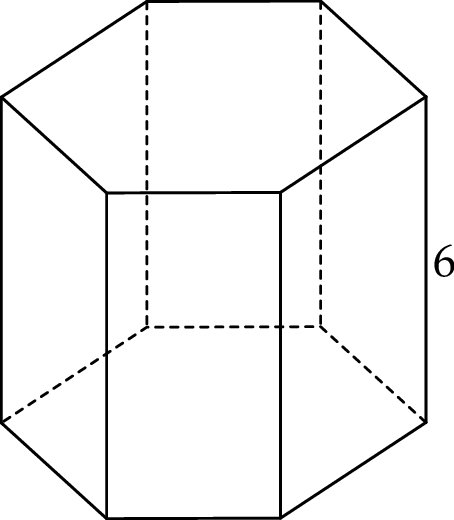
Pole podstawy tego graniastosłupa jest równe 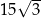 . Pole jednej ściany bocznej tego graniastosłupa jest równe
. Pole jednej ściany bocznej tego graniastosłupa jest równe
A) 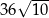 B) 60 C)
B) 60 C) 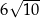 D) 360
D) 360
Kąt nachylenia najdłuższej przekątnej graniastosłupa prawidłowego sześciokątnego do płaszczyzny podstawy jest zaznaczony na rysunku
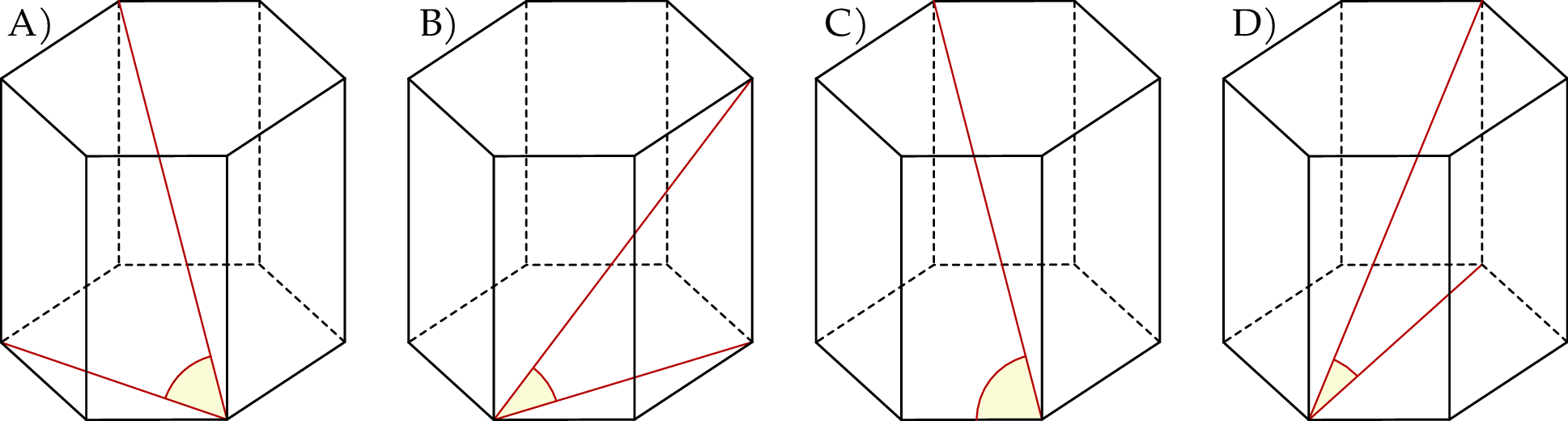
Objętość ostrosłupa prawidłowego czworokątnego jest równa 64. Wysokość tego ostrosłupa jest równa 12. Długość krawędzi podstawy tego ostrosłupa jest równa
A) 2 B) 4 C) 6 D) 8
Rozważamy wszystkie kody czterocyfrowe utworzone tylko z cyfr 1, 3, 6, 8, przy czym w każdym kodzie każda z tych cyfr występuje dokładnie jeden raz. Liczba wszystkich takich kodów jest równa
A) 4 B) 10 C) 24 D) 16
Zadania otwarte
Rozwiąż nierówność: 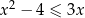 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 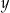 takich, że
takich, że 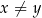 , prawdziwa jest nierówność
, prawdziwa jest nierówność
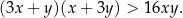
Osią symetrii wykresu funkcji kwadratowej 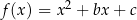 jest prosta o równaniu
jest prosta o równaniu 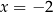 . Jednym z miejsc zerowych funkcji
. Jednym z miejsc zerowych funkcji 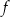 jest liczba 1. Oblicz współczynniki
jest liczba 1. Oblicz współczynniki 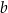 oraz
oraz  .
.
Ciąg arytmetyczny 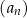 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 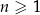 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy 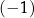 , a suma piętnastu początkowych kolejnych wyrazów tego ciągu jest równa
, a suma piętnastu początkowych kolejnych wyrazów tego ciągu jest równa 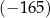 . Oblicz różnicę tego ciągu.
. Oblicz różnicę tego ciągu.
W kartezjańskim układzie współrzędnych 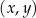 dany jest równoległobok
dany jest równoległobok 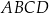 , w którym
, w którym 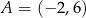 oraz
oraz 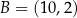 . Przekątne
. Przekątne 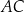 oraz
oraz 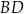 tego równoległoboku przecinają się w punkcie
tego równoległoboku przecinają się w punkcie 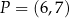 . Oblicz długość boku
. Oblicz długość boku 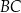 tego równoległoboku.
tego równoległoboku.
Dany jest pięcioelementowy zbiór 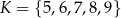 . Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru
. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru 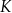 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia 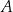 polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
W graniastosłupie prawidłowym czworokątnym o objętości równej 108 stosunek długości krawędzi podstawy do wysokości graniastosłupa jest równy  . Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem  (zobacz rysunek).
(zobacz rysunek).
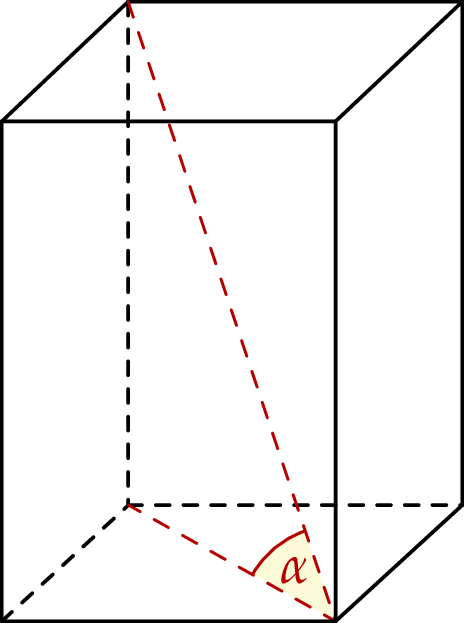
Oblicz cosinus kąta  oraz pole powierzchni całkowitej tego graniastosłupa.
oraz pole powierzchni całkowitej tego graniastosłupa.

