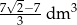Zadanie nr 2837073
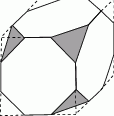
W kostce mającej kształt sześcianu o boku 1 dm ścięto wszystkie naroża w ten sposób ze wszystkie krawędzie nowopowstałej bryły mają tę samą długość. Obliczyć objętość otrzymanej bryły.
Rozwiązanie
Zacznijmy od rysunku.
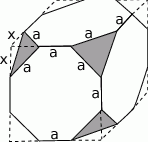
Oznaczmy przez  długość krawędzi w nowopowstałej bryle, oraz przez
długość krawędzi w nowopowstałej bryle, oraz przez  długość krawędzi bocznej w odciętym narożu. Mamy wtedy równania
długość krawędzi bocznej w odciętym narożu. Mamy wtedy równania
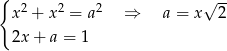
Podstawiając wyliczoną wartość  z pierwszego równania do drugiego, mamy
z pierwszego równania do drugiego, mamy
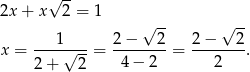
Objętość tej bryły najłatwiej obliczyć odejmując od objętości sześcianu objętość odciętych naroży. Na każde naroże możemy patrzeć jak na ostrosłup, który w podstawie ma trójkąt prostokątny o przyprostokątnych długości  , i który ma wysokość długości
, i który ma wysokość długości  . Objętość takiego ostrosłupa jest równa
. Objętość takiego ostrosłupa jest równa
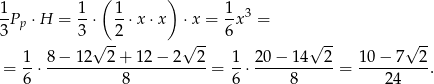
Zatem objętość bryły jest równa
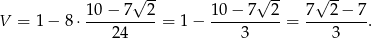
Odpowiedź: