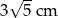Zadanie nr 3261363
Oblicz długość przeciwprostokątnej trójkąta prostokątnego, wiedząc, że objętość brył powstałych z obrotu tego trójkąta wokół przyprostokątnych wynoszą odpowiednio 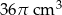 i
i 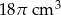 .
.
Rozwiązanie
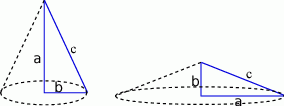
Jeżeli naszkicujemy sobie bryły powstałe w wyniku opisanego obrotu to widać, że są to dwa stożki o promieniu podstawy i wysokości równej odpowiednio  i
i  oraz
oraz 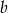 i
i  , gdzie
, gdzie 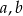 - długości przyprostokątnych trójkąta.
- długości przyprostokątnych trójkąta.
Ze wzoru na obiętość stożka mamy zatem
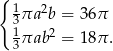
Podzielmy pierwsze równanie przez drugie stronami.
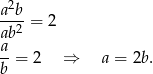
Podstawmy tę wartość do drugiego równania
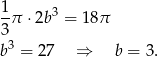
Zatem 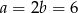 . Długość przeciwprostokątnej obliczamy z twierdzenia Pitagorasa.
. Długość przeciwprostokątnej obliczamy z twierdzenia Pitagorasa.
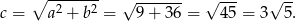
Odpowiedź: