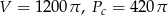Zadanie nr 3565554
Trójkąt prostokątny o przyprostokątnych 15 i 20 obraca się wokół przeciwprostokątnej. Oblicz objętość i pole powierzchni całkowitej tej bryły.
Rozwiązanie
Zaczynamy od rysunku. Od razu rysujemy przekrój osiowy otrzymanej bryły.
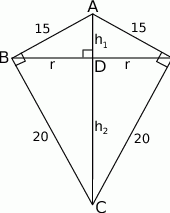
Widać, że otrzymana bryła składa się z dwóch stożków o wspólnej podstawie, której promień  jest równy wysokości wyjściowego trójkąta prostokątnego opuszczonej na przeciwprostokątną. Wysokości tych stożków w sumie dają długość przeciwprostokątnej, czyli
jest równy wysokości wyjściowego trójkąta prostokątnego opuszczonej na przeciwprostokątną. Wysokości tych stożków w sumie dają długość przeciwprostokątnej, czyli
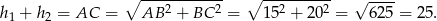
Długość promienia  możemy obliczyć z porównania dwóch wzorów na pole.
możemy obliczyć z porównania dwóch wzorów na pole.
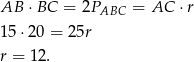
Długość promienia  mogliśmy też obliczyć wykorzystując podobieństwo trójkątów
mogliśmy też obliczyć wykorzystując podobieństwo trójkątów 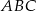 i
i 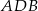 .
.
Możemy teraz policzyć objętość otrzymanej bryły.
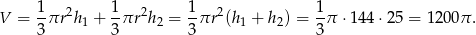
Liczymy jeszcze pole powierzchni (ze wzoru na pole powierzchni bocznej stożka).
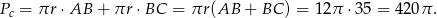
Odpowiedź: