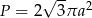/Szkoła średnia/Geometria/Stereometria/Inne bryły

Zadanie nr 6278003

Dodaj do ulubionych
Dodaj do rozwiązanych

Romb o kącie ostrym 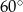∘ 60 , obraca się wokół boku. Oblicz pole powierzchni i objętość otrzymanej bryły wiedząc że długość boku rombu jest równa a .

Rozwiązanie

Gdy naszkicujemy sobie opisaną sytuację, widać, że otrzymana bryła to walec, z którego z prawej strony wycięty jest stożek, i taki sam stożek jest przyklejony z lewej strony.

PIC

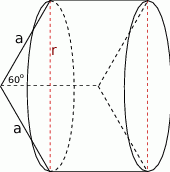
Ponieważ stożki te są przystające, objętość tej bryły to dokładnie objętość walca (tyle samo wycinamy co przyklejamy). Wysokość tego walca to a , pozostało zatem wyliczyć promień r jego podstawy. Robimy to korzystając z podanego kąta ostrego rombu.

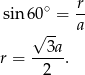
∘ r- sin 60 = a √ -- r = --3a-. 2

Liczymy objętość

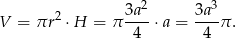
2 3 V = πr2 ⋅H = π 3a--⋅a = 3a--π . 4 4

Pole powierzchni otrzymanej bryły to suma pola powierzchni bocznej walca i podwojonej powierzchni bocznej stożka, zatem

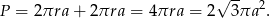
√ -- P = 2πra + 2πra = 4πra = 2 3πa 2.

 
Odpowiedź: 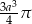3a3π 4 , √ -- P = 2 3πa 2

Wersja PDF