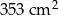Zadanie nr 9201283

Spawacz ma wykonać z blachy konstrukcję, która powstaje przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego trójkątnego. Wymiary elementów są podane na rysunku.

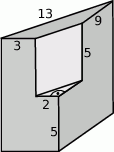
Oblicz objętość tej konstrukcji.
Oblicz łączne pole powierzchni wszystkich 7 ścian otrzymanej bryły. Wynik podaj z zaokrągleniem do .

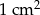Rozwiązanie

Oznaczmy wierzchołki danej bryły tak, aby móc łatwo się do nich odnosić.

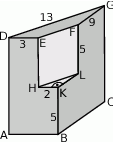
Zauważmy, że 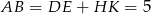, więc możemy wyliczyć długość krawędzi z twierdzenia Pitagorasa.
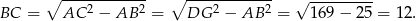
$∘ ------------ ∘ ------------ √ --------- BC = AC 2 − AB 2 = DG 2 − AB 2 = 169− 25 = 12 .$

Stąd

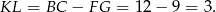
$KL = BC − FG = 12 − 9 = 3.$

Zauważmy też, że .
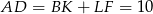Mamy już wszystkie długości odcinków potrzebne do wyliczenia objętości danej bryły. Objętość dużego graniastosłupa, przed wycięciem małego, jest równa

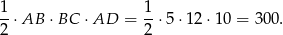
$1 1 --⋅AB ⋅BC ⋅AD = --⋅5 ⋅12⋅ 10 = 300 . 2 2$

Od tej objętości trzeba odjąć objętość wyciętego graniastosłupa, która jest równa

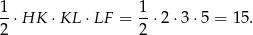
$1 1 --⋅HK ⋅ KL ⋅LF = --⋅2 ⋅3 ⋅5 = 15. 2 2$

Zatem szukana objętość jest równa

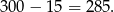
$300 − 15 = 2 85.$

Odpowiedź: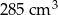
Zacznijmy od obliczenia pola powierzchni dużego graniastosłupa przed wycięciem małego.
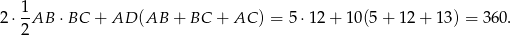
$1- 2⋅ 2AB ⋅BC + AD (AB + BC + AC ) = 5 ⋅12+ 10(5 + 12 + 13) = 360.$

Jak się to pole różni od pola otrzymanej bryły? – trzeba odjąć pola prostokątów o bokach 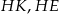oraz 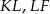, a potem dodać pole prostokąta 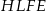. Zauważmy, że trójkąt 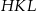dokładnie odpowiada trójkątowi wyciętemu u góry, więc możemy nie brać go pod uwagę.
Zacznijmy od policzenia długości odcinka 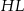(z twierdzenia Pitagorasa).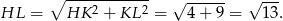

$∘ ------------ √ ------ √ --- HL = HK 2 + KL 2 = 4+ 9 = 13.$

Zatem szukane pole powierzchni jest równe

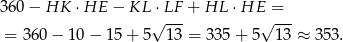
$360 − HK ⋅HE − KL ⋅LF + HL ⋅HE = √ --- √ --- = 360 − 1 0− 15+ 5 13 = 33 5+ 5 13 ≈ 353 .$

Odpowiedź: