/Szkoła średnia/Geometria/Stereometria/Inne bryły

Zadanie nr 9489163

Dodaj do ulubionych
Dodaj do rozwiązanych

Kwadrat o boku długości 2 cm obraca się wokół swojej przekątnej. Oblicz objętość i pole powierzchni otrzymanej bryły.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

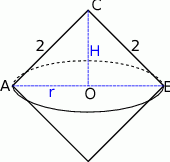
Widać, że otrzymana bryła to dwa sklejone podstawami stożki. Zarówno wysokość jak i promień podstawy tych stożków to dokładnie połowa długości przekątnej kwadratu, czyli

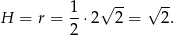
1- √ -- √ -- H = r = 2 ⋅ 2 2 = 2.

Zatem objętość bryły jest równa

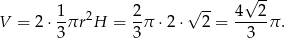
√ -- 1- 2 2- √ -- 4--2- V = 2 ⋅3 πr H = 3π ⋅2 ⋅ 2 = 3 π .

Pole powierzchni to podwojone pole powierzchni bocznej stożka, czyli

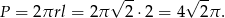
√ -- √ -- P = 2πrl = 2π 2⋅ 2 = 4 2π .

 
Odpowiedź: √ - -- V = 4--2π cm 3, P = 4√ 2 π cm 2 3

Wersja PDF