/Szkoła średnia/Zadania maturalne/Matura 2024/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 20 kwietnia 2024 Czas pracy: 180 minut
Funkcja 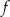 o dziedzinie
o dziedzinie 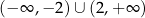 jest określona jako nieskończona suma
jest określona jako nieskończona suma
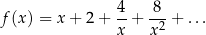
Wykres funkcji 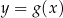 powstaje z wykresu funkcji
powstaje z wykresu funkcji 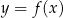 przez przesunięcie o wektor
przez przesunięcie o wektor ![[− 2,− 2]](https://img.zadania.info/zes/0055954/HzesT5x.png) . Rozwiąż nierówność
. Rozwiąż nierówność 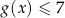 .
.
W skład pociągu osobowego wchodzi lokomotywa (która znajduje się na początku składu) i 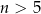 wagonów osobowych, wśród których są dokładnie trzy wagony pierwszej klasy. Liczba takich ustawień kolejności wagonów, w których trzy wagony pierwszej klasy znajdują się bezpośrednio za sobą jest 12 razy mniejsza niż liczba ustawień wagonów, w których żaden z wagonów pierwszej klasy nie znajduje się ani na końcu pociągu ani bezpośrednio za lokomotywą. Oblicz
wagonów osobowych, wśród których są dokładnie trzy wagony pierwszej klasy. Liczba takich ustawień kolejności wagonów, w których trzy wagony pierwszej klasy znajdują się bezpośrednio za sobą jest 12 razy mniejsza niż liczba ustawień wagonów, w których żaden z wagonów pierwszej klasy nie znajduje się ani na końcu pociągu ani bezpośrednio za lokomotywą. Oblicz  .
.
Funkcja 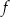 jest określona wzorem
jest określona wzorem 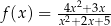 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 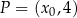 należy do wykresu funkcji
należy do wykresu funkcji 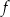 . Oblicz
. Oblicz 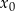 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 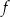 w punkcie
w punkcie 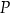 .
.
Udowodnij, że dla dowolnych liczb dodatnich  i
i 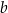 prawdziwa jest nierówność
prawdziwa jest nierówność
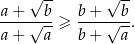
Bok rombu 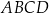 ma długość
ma długość  , a sinus jego kąta ostrego
, a sinus jego kąta ostrego 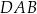 jest równy
jest równy 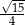 . Na bokach
. Na bokach 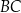 i
i 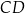 wybrano punkty
wybrano punkty 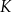 i
i 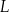 odpowiednio tak, że odcinki
odpowiednio tak, że odcinki 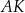 i
i 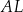 podzieliły pole rombu
podzieliły pole rombu  na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).
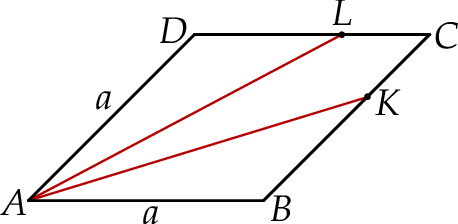
Oblicz długość odcinka 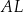 .
.
Dany jest sześcian 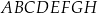 o krawędzi długości 1. Punkty
o krawędzi długości 1. Punkty 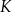 i
i 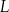 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 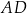 i
i 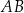 , a punkt
, a punkt 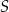 jest środkiem odcinka
jest środkiem odcinka 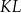 . Punkt
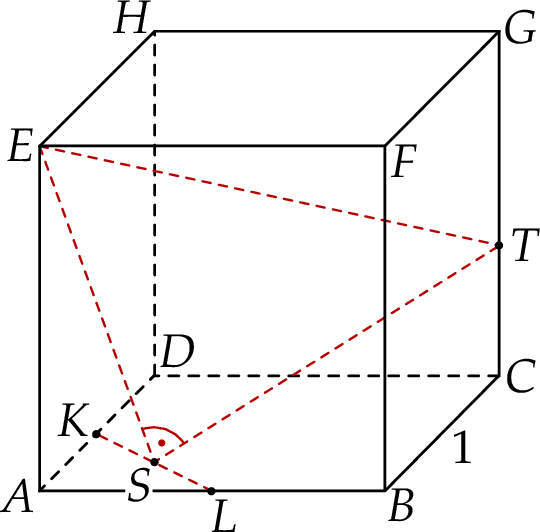
. Punkt 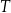 jest takim punktem krawędzi
jest takim punktem krawędzi 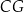 , że
, że 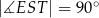 (zobacz rysunek).
(zobacz rysunek).
Oblicz odległość punktu 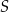 od środka odcinka
od środka odcinka 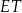 .
.
Rozwiąż równanie 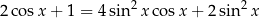 , dla
, dla ![x ∈ [0,2π ]](https://img.zadania.info/zes/0055954/HzesT47x.png) .
.
Trapez równoramienny 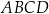 nie jest równoległobokiem. Przekątna
nie jest równoległobokiem. Przekątna 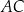 tego trapezu tworzy z podstawą
tego trapezu tworzy z podstawą 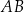 kąt o mierze
kąt o mierze 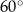 . Wykaż, że trapez
. Wykaż, że trapez 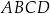 nie może być opisany na okręgu.
nie może być opisany na okręgu.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 27. Jeśli największą z tych liczb zwiększymy o 12, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Wyznacz wszystkie wartości parametru 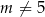 , dla których równanie
, dla których równanie
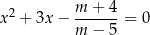
ma dwa różne rozwiązania rzeczywiste 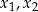 spełniające warunek
spełniające warunek 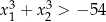 .
.
Oblicz prawdopodobieństwo tego, że trzy losowo wybrane wierzchołki sześcianu są wierzchołkami trójkąta równobocznego.
Punkty 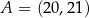 i
i 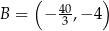 są końcami przeciwprostokątnej trójkąta prostokątnego
są końcami przeciwprostokątnej trójkąta prostokątnego 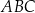 . Punkt
. Punkt 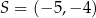 jest środkiem okręgu wpisanego w ten trójkąt. Oblicz pole trójkąta
jest środkiem okręgu wpisanego w ten trójkąt. Oblicz pole trójkąta 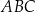 .
.
Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma długości wszystkich krawędzi jest równa 6.
-
Wyznacz zależność objętości
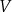 ostrosłupa od jego krawędzi podstawy
ostrosłupa od jego krawędzi podstawy  i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 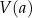 .
. -
Wyznacz długość krawędzi podstawy tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tą największą objętość.

