/Szkoła średnia/Zadania maturalne/Matura 2024/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 23 marca 2024 Czas pracy: 180 minut
Największą liczbą naturalną, która spełnia nierówności 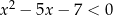 jest
jest
A) 0 B) 3 C) 7 D) 6
Liczba 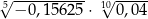 jest równa
jest równa
A) 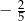 B)
B) 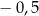 C)
C) 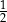 D)
D) 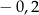
Różnica 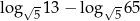 jest równa
jest równa
A)  B)
B) 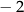 C) 2 D)
C) 2 D) 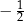
Na osi liczbowej zaznaczono przedział.

Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A) 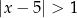 B)
B) 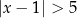 C)
C) 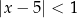 D)
D) 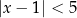
Informacja do zadań 5.1 i 5.2
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji  (zobacz rysunek).
(zobacz rysunek).
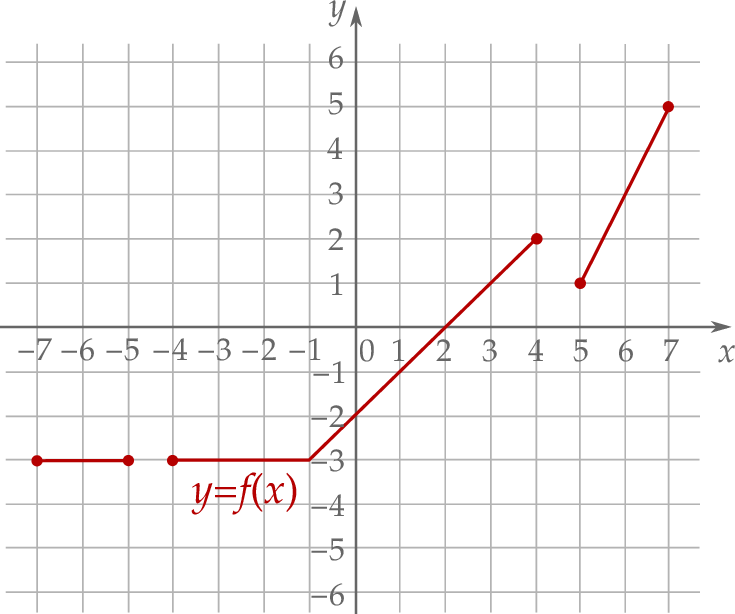
Wyznacz zbiór wszystkich argumentów, dla których funkcja 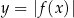 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
Funkcja 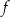 jest rosnąca w przedziale
jest rosnąca w przedziale
A) ![[− 4,4]](https://img.zadania.info/zes/0063637/HzesT20x.png) B)
B) ![[− 1,7]](https://img.zadania.info/zes/0063637/HzesT21x.png) C)
C) ![[5,7]](https://img.zadania.info/zes/0063637/HzesT22x.png) D)
D) ![[− 4,7]](https://img.zadania.info/zes/0063637/HzesT23x.png)
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 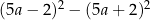 jest równe
jest równe
A) 0 B) 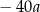 C) 8 D)
C) 8 D) 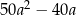
Wykaż, że dla każdej liczby naturalnej  reszta z dzielenia liczby
reszta z dzielenia liczby 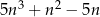 przez
przez 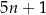 jest równa 1.
jest równa 1.
W kartezjańskim układzie współrzędnych 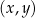 dane są proste
dane są proste 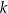 oraz
oraz 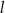 o równaniach
o równaniach
Dokończ zdanie. Wybierz odpowiedź A albo B oraz odpowiedź 1., 2. albo 3.
Proste 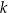 oraz
oraz 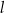
| A) są prostopadłe | B) nie są prostopadłe |
i przecinają się w punkcie 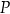 o współrzędnych
o współrzędnych
1. 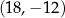 | 2. 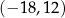 | 3. 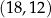 |
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
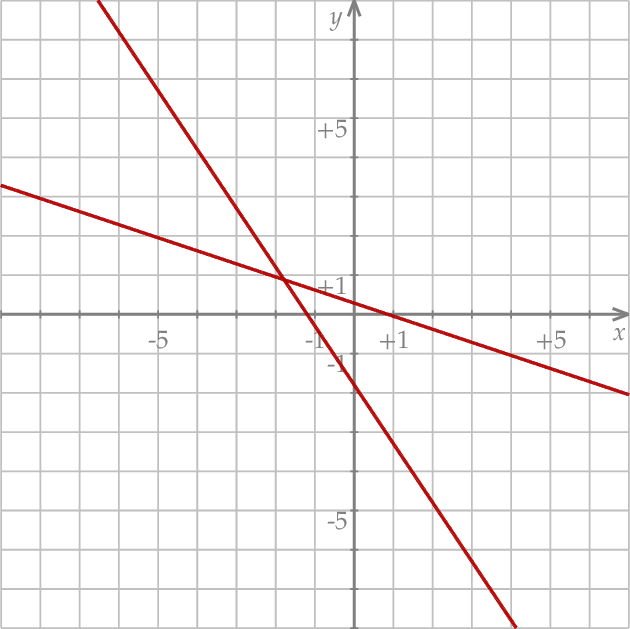
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 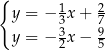 B)
B) 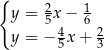 C)
C) 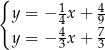 D)
D) 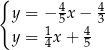
Dany jest wielomian 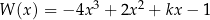 , gdzie
, gdzie 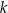 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 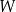 można zapisać w postaci
można zapisać w postaci 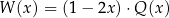 dla pewnego wielomianu
dla pewnego wielomianu 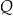 . Liczba
. Liczba 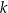 jest równa
jest równa
A) 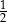 B) 2 C)
B) 2 C) 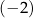 D)
D) 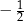
Proces stygnięcia herbaty w otoczeniu o stałej temperaturze 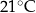 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 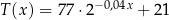 , gdzie
, gdzie 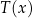 to temperatura herbaty wyrażona w stopniach Celsjusza po
to temperatura herbaty wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 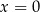 , w którym herbatę zalano wrzątkiem. Temperatura herbaty po 25 minutach od momentu zalania wrzątkiem jest równa
, w którym herbatę zalano wrzątkiem. Temperatura herbaty po 25 minutach od momentu zalania wrzątkiem jest równa
A) 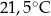 B)
B) 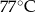 C)
C) 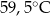 D)
D) 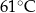
Dla każdej liczby rzeczywistej  różnej od 0 i
różnej od 0 i 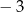 wyrażenie
wyrażenie 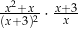 jest równe
jest równe
A) 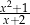 B)
B) 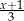 C)
C) 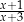 D)
D) 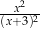
Jednym z miejsc zerowych funkcji kwadratowej 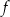 jest liczba
jest liczba 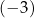 . Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji
. Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji 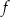 , jest równa 3. Drugim miejscem zerowym funkcji
, jest równa 3. Drugim miejscem zerowym funkcji 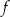 jest liczba
jest liczba
A) 6 B) 5 C) 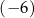 D) 9
D) 9
Ciąg 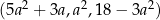 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
W kartezjańskim układzie współrzędnych 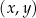 zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 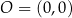 . Jedno z ramion tego kąta pokrywa się z ujemną półosią
. Jedno z ramion tego kąta pokrywa się z ujemną półosią 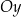 , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 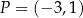 (zobacz rysunek).
(zobacz rysunek).
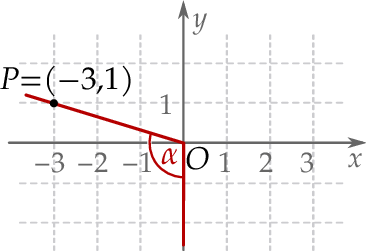
Tangens kąta  jest równy
jest równy
A) 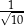 B)
B) 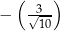 C)
C) 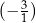 D)
D) 
Wskaż równanie, którego rozwiązaniami są liczby 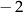 oraz 3.
oraz 3.
A) 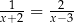 B)
B) 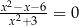 C)
C) 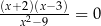 D)
D) 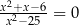
Funkcje  oraz
oraz  są określone dla każdej liczby rzeczywistej
są określone dla każdej liczby rzeczywistej  . Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Liczba 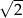 jest wartością funkcji
jest wartością funkcji
A) 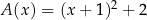 B)
B) 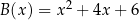 C)
C) 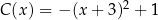
D) 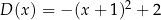 E)
E) 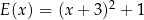 F)
F) 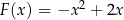
Informacja do zadań 18.1 i 18.2
Na rysunkach A–F w kartezjańskim układzie współrzędnych  zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią  , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:  lub
lub 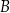 , lub
, lub 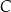 , lub
, lub 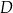 , lub
, lub 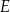 , lub
, lub  .
.
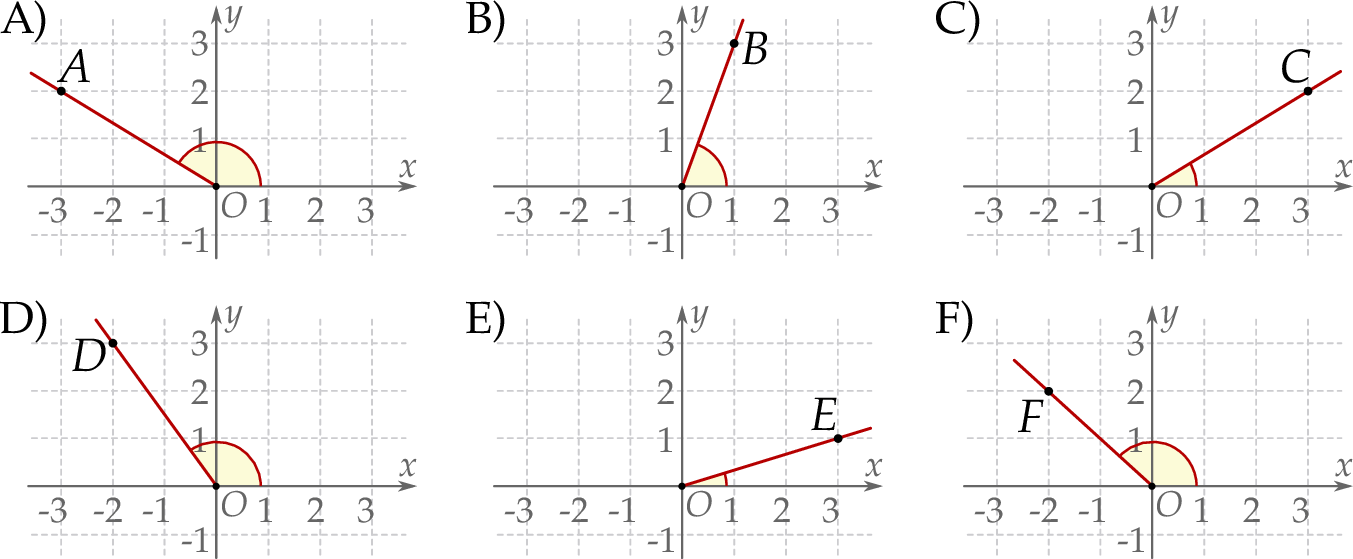
Na którym z rysunków zaznaczono kąt  , spełniający warunek
, spełniający warunek  ?
?
Na którym z rysunków zaznaczono kąt 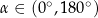 , spełniający warunek
, spełniający warunek 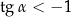 ?
?
Okrąg  o środku
o środku 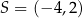 jest styczny do osi
jest styczny do osi 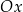 układu współrzędnych. Okrąg
układu współrzędnych. Okrąg  jest określony równaniem
jest określony równaniem
A) 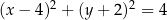 B)
B) 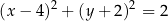
C) 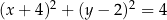 D)
D) 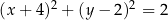
Zakład stolarski produkuje stoły, które sprzedaje po 2144 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:
-
przychód
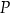 (w złotych) ze sprzedaży
(w złotych) ze sprzedaży  stołów można opisać funkcją
stołów można opisać funkcją 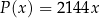
-
koszt
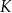 (w złotych) produkcji
(w złotych) produkcji  stołów miesięcznie można opisać funkcją
stołów miesięcznie można opisać funkcją 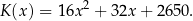
Miesięcznie w zakładzie można wyprodukować co najwyżej 80 stołów. Oblicz, ile stołów powinien miesięcznie sprzedawać zakład, aby zysk ze sprzedaży stołów wyprodukowanych przez ten zakład w ciągu jednego miesiąca był możliwie największy. Oblicz ten największy zysk.
Ciąg 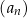 jest określony wzorem
jest określony wzorem 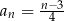 dla każdej liczby naturalnej
dla każdej liczby naturalnej 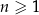 . Liczba wyrazów tego ciągu mniejszych od 10 jest równa
. Liczba wyrazów tego ciągu mniejszych od 10 jest równa
A) 43 B) 37 C) 36 D) 42
Wszystkich różnych liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym są dokładnie 3 takie same cyfry jest
A) 400 B) 360 C) 288 D) 324
Rozwiąż równanie 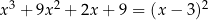 .
.
Pole czworokąta 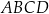 jest równe
jest równe 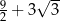 . Ponadto:
. Ponadto: 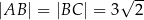 ,
, 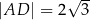 ,
, 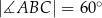 ,
, 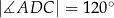 (zobacz rysunek).
(zobacz rysunek).
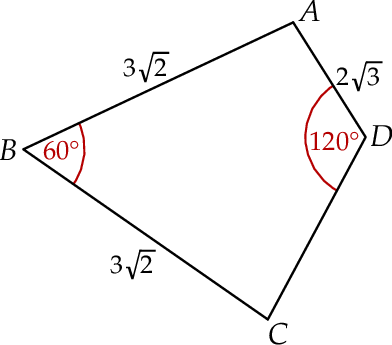
Długość boku 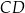 jest równa
jest równa
A) 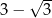 B)
B) 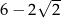 C)
C) 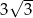 D)
D) 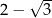
Suma trzech pierwszych wyrazów malejącego ciągu geometrycznego jest równa 10,5. Drugi wyraz tego ciągu jest równy 3. Czwarty wyraz tego ciągu jest równy
A) 1,5 B) 3,5 C) 0,75 D) 2,25
W okręgu 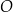 kąt środkowy
kąt środkowy 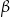 jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany
jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany  . Kąt
. Kąt 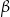 ma miarę o
ma miarę o 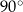 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 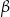 jest równa
jest równa
A) 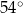 B)
B) 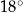 C)
C) 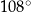 D)
D) 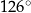
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą dwucyfrową, jest równe
A)  B)
B) 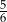 C)
C) 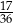 D)
D) 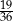
Funkcja 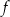 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 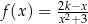 , gdzie
, gdzie 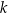 jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek
jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek 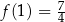 . Wartość współczynnika
. Wartość współczynnika 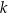 we wzorze tej funkcji jest równa
we wzorze tej funkcji jest równa
A) 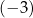 B) 3 C)
B) 3 C) 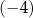 D) 4
D) 4
Na bokach 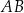 i
i 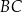 trójkąta
trójkąta 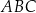 wybrano odpowiednio punkty
wybrano odpowiednio punkty 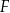 i
i 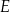 w ten sposób, że
w ten sposób, że 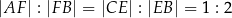 . Odcinki
. Odcinki 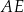 i
i 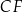 przecinają się w punkcie
przecinają się w punkcie 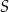 (zobacz rysunek).
(zobacz rysunek).
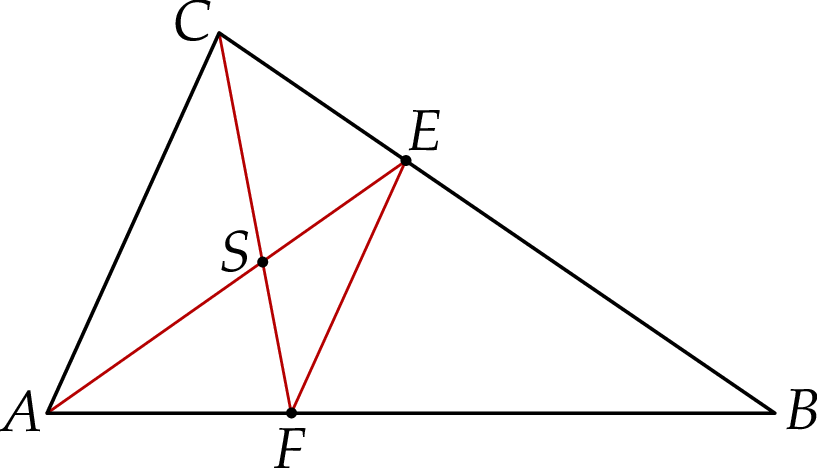
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 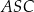 jest podobny do trójkąta jest podobny do trójkąta 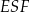 . . | P | F |
Pole trójkąta 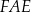 jest równe polu trójkąta jest równe polu trójkąta 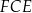 . . | P | F |
Dany jest graniastosłup prawidłowy sześciokątny 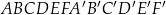 , w którym krawędź podstawy ma długość 3. Przekątna
, w którym krawędź podstawy ma długość 3. Przekątna 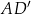 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 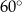 (zobacz rysunek).
(zobacz rysunek).
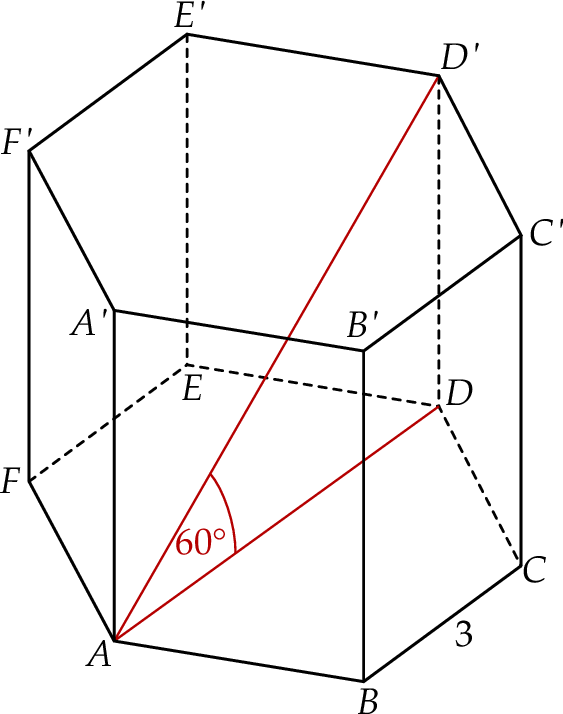
Pole ściany bocznej tego graniastosłupa jest równe
A) 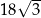 B)
B) 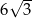 C)
C) 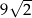 D) 90
D) 90
Dany jest okrąg 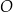 o środku w punkcie
o środku w punkcie 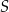 . Przedłużenie średnicy
. Przedłużenie średnicy 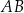 tego okręgu przecina przedłużenie cięciwy
tego okręgu przecina przedłużenie cięciwy 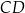 w punkcie
w punkcie 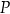 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 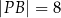 ,
, 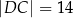 oraz
oraz 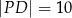 .
.
Oblicz promień okręgu 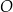 .
.
Mediana kolejnych sześciu liczb naturalnych jest równa 47,5. Najmniejsza z tych liczb to
A) 46 B) 41 C) 45 D) 44
Punkty 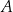 oraz
oraz 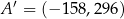 są symetryczne względem prostej
są symetryczne względem prostej 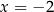 . Wówczas
. Wówczas
A) 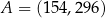 B)
B) 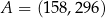 C)
C) 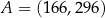 D)
D) 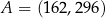
Ze zbioru sześciu liczb 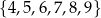 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 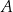 polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 9.
polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 9.

