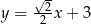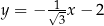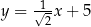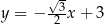/Szkoła średnia/Zadania maturalne/Matura 2024/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 9 marca 2024 Czas pracy: 180 minut
Wszystkich liczb całkowitych spełniających nierówność 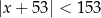 jest
jest
A) 305 B) 304 C) 307 D) 100
W klasie jest o 15% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 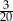 B)
B) 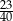 C)
C) 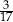 D)
D) 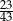
Liczba 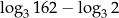 jest równa
jest równa
A) 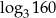 B)
B) 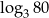 C) 4 D) 5
C) 4 D) 5
Liczba 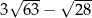 jest równa
jest równa
A) 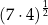 B)
B) 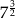 C) 7 D)
C) 7 D) 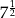
Liczba 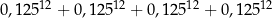 jest równa
jest równa
A) 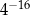 B)
B) 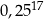 C)
C) 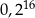 D)
D) 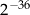
Liczba 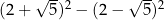 jest równa
jest równa
A) 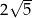 B)
B) 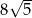 C)
C) 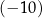 D)
D) 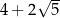
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 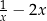 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 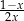 C)
C) 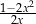 D)
D) 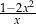
Równanie
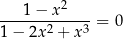
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie 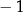 .
.
C) ma dokładnie jedno rozwiązanie 1.
D) ma dokładnie dwa rozwiązania 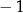 oraz 1.
oraz 1.
Wykaż, że dla każdej liczby naturalnej 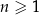 liczba
liczba 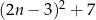 jest podzielna przez 8.
jest podzielna przez 8.
Dany jest układ równań
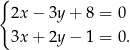
Rozwiązaniem tego układu równań jest para liczb
A) 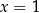 i
i 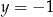 B)
B) 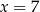 i
i 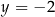 C)
C) 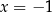 i
i 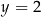 D)
D) 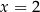 i
i 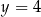
W kartezjańskim układzie współrzędnych 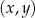 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami czworokąta 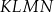 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Czworokąt 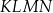 jest
jest
| A) | prostokątem, |
| B) | trapezem, który nie jest równoległobokiem |
| C) | równoległobokiem, który nie jest prostokątem, |
ponieważ
| 1) | czworokąt 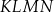 ma dwie osie symetrii. ma dwie osie symetrii. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | dwie z tych prostych są równoległe. |
Informacja do zadań 12.1 – 12.3
W kartezjańskim układzie współrzędnych 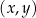 narysowano wykres funkcji
narysowano wykres funkcji 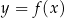 (zobacz rysunek).
(zobacz rysunek).
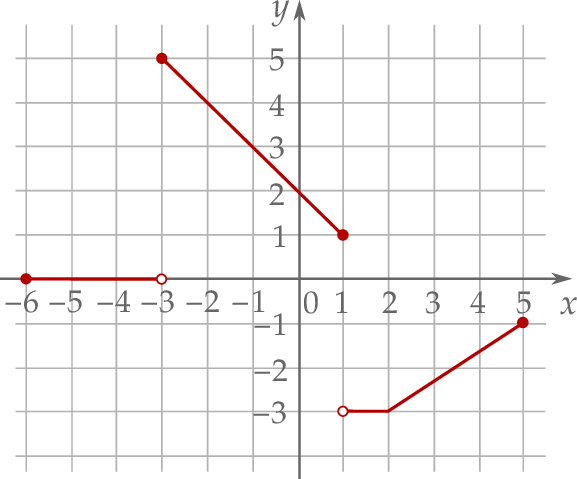
Dziedziną funkcji 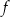 jest zbiór
jest zbiór
A) 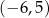 B)
B) ![[− 6,5 ]](https://img.zadania.info/zes/0088481/HzesT55x.png) C)
C) ![(− 3,5]](https://img.zadania.info/zes/0088481/HzesT56x.png) D)
D) ![[− 3,5 ]](https://img.zadania.info/zes/0088481/HzesT57x.png)
Największa wartość funkcji 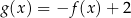 w przedziale
w przedziale ![[− 4,1]](https://img.zadania.info/zes/0088481/HzesT59x.png) jest równa
jest równa
A) 2 B) 5 C) 7 D) 3
Funkcja 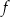 jest rosnąca w zbiorze
jest rosnąca w zbiorze
A) 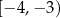 B)
B) ![[2,5]](https://img.zadania.info/zes/0088481/HzesT62x.png) C)
C) ![(1,5]](https://img.zadania.info/zes/0088481/HzesT63x.png) D)
D) ![[−3 ,1]](https://img.zadania.info/zes/0088481/HzesT64x.png)
Ciąg 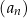 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 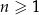 . Suma
. Suma  początkowych wyrazów tego ciągu jest określona wzorem
początkowych wyrazów tego ciągu jest określona wzorem
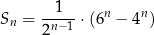
dla każdej liczby naturalnej 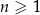 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trzeci wyraz ciągu 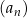 jest równy 28. jest równy 28. | P | F |
Wśród wyrazów ciągu 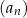 jest liczba 2025. jest liczba 2025. | P | F |
Wyznacz wszystkie liczby ujemne  spełniające nierówność
spełniające nierówność 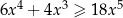 .
.
Funkcja liniowa 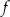 jest określona wzorem
jest określona wzorem 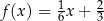 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Miejscem zerowym funkcji 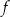 jest liczba jest liczba 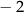 . . | P | F |
Punkt przecięcia wykresu funkcji 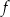 z osią z osią 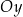 ma współrzędne ma współrzędne 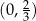 . . | P | F |
Trzywyrazowy ciąg 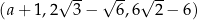 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 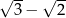 B)
B) 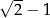 C)
C) 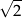 D)
D) 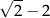
Dany jest trójkąt, którego kąty mają miary 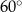 ,
, 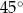 oraz
oraz 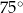 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 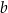 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).
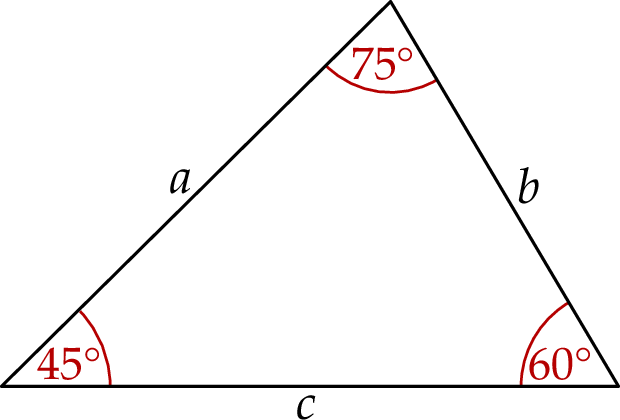
Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 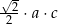 B)
B) 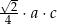 C)
C) 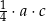
D) 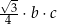 E)
E) 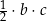 F)
F) 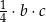
Dana jest prosta 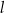 o równaniu
o równaniu 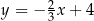 . Prosta
. Prosta 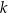 jest prostopadła do prostej
jest prostopadła do prostej 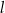 i przechodzi przez punkt
i przechodzi przez punkt 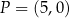 . Prosta
. Prosta 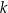 ma równanie
ma równanie
A) 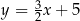 B)
B) 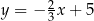 C)
C) 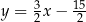 D)
D) 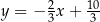
W rombie o boku długości 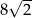 kąt rozwarty ma miarę
kąt rozwarty ma miarę 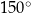 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy
A) 128 B) 24 C) 64 D) 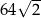
Z kawałka blachy należy wyciąć figurę w kształcie trapezu prostokątnego. Dłuższa podstawa trapezu ma mieć długość 6 dm, a suma długości krótszej podstawy i wysokości tego trapezu ma być równa 16 dm. Oblicz, jaką długość powinna mieć krótsza podstawa tego trapezu, tak aby pole powierzchni figury było największe. Oblicz to pole.
Prostokąt 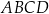 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 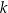 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 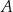 i tworzy z odcinkiem
i tworzy z odcinkiem 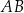 kąt o mierze
kąt o mierze  . Przekątne prostokąta
. Przekątne prostokąta 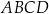 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze 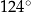 (zobacz rysunek).
(zobacz rysunek).
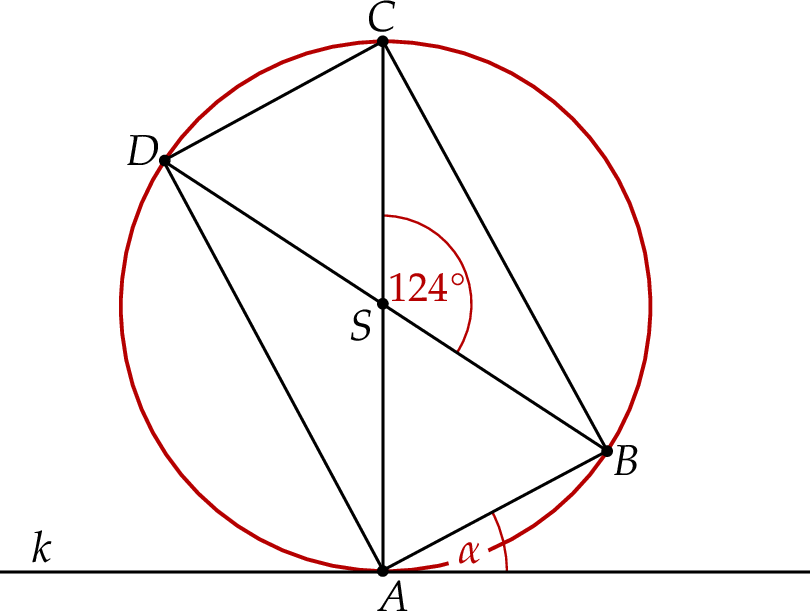
Miara kąta  jest równa
jest równa
A) 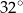 B)
B) 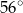 C)
C) 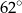 D)
D) 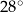
W prostokącie 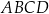 dane są wierzchołki
dane są wierzchołki 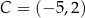 oraz
oraz 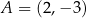 . Bok
. Bok 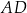 ma długość 5. Pole tego prostokąta jest równe
ma długość 5. Pole tego prostokąta jest równe
A) 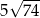 B) 35 C)
B) 35 C) 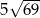 D) 245
D) 245
W kartezjańskim układzie współrzędnych 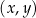 dana jest prosta
dana jest prosta 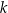 o równaniu
o równaniu 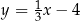 . Prosta o równaniu
. Prosta o równaniu 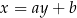 jest równoległa do prostej
jest równoległa do prostej 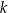 i przechodzi przez punkt
i przechodzi przez punkt 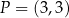 , gdy
, gdy
A) 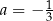 i
i 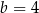 B)
B) 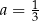 i
i 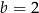 C)
C) 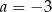 i
i 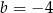 D)
D) 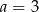 i
i 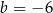
Rozwiąż równanie 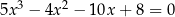 .
.
Punkty 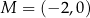 i
i 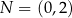 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 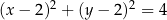 B)
B) 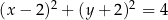
C) 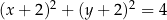 D)
D) 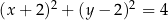
Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0, 3, 5, 7, jest
A) 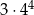 B)
B) 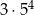 C)
C) 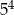 D)
D) 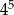
Czterowyrazowy ciąg 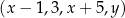 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba 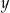 jest równa
jest równa
A) 6 B) 7 C) 13 D) 9
Funkcja kwadratowa 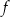 jest określona wzorem
jest określona wzorem 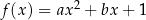 , gdzie
, gdzie  oraz
oraz 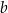 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 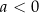 i
i 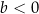 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 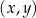 . Fragment wykresu funkcji
. Fragment wykresu funkcji 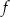 przedstawiono na rysunku
przedstawiono na rysunku
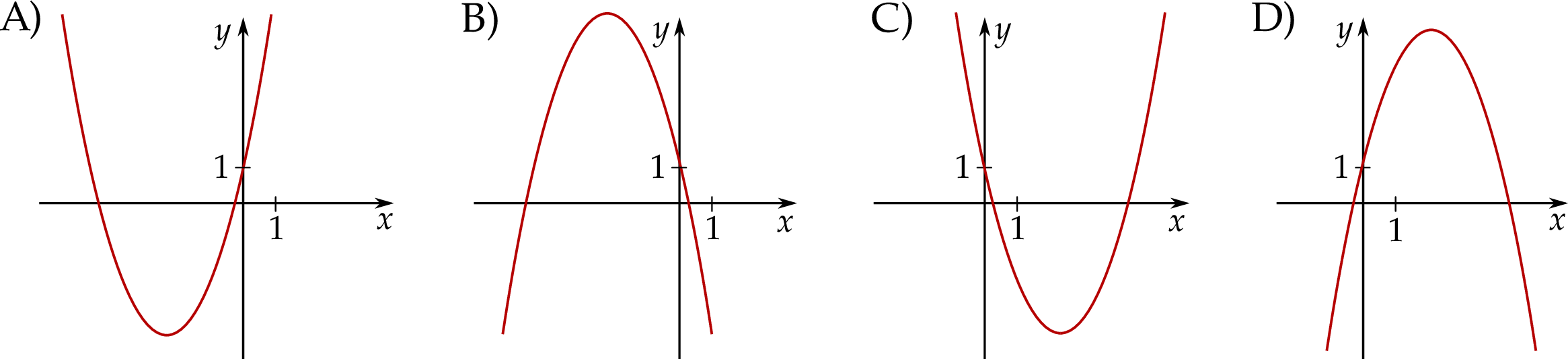
Informacja do zadań 29.1 i 29.2
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 5. Jedna z krawędzi bocznych tego ostrosłupa ma długość 9 i jest prostopadła do płaszczyzny podstawy.
Oblicz objętość tego ostrosłupa.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Każda ze ścian bocznych ostrosłupa jest trójkątem prostokątnym. | P | F |
Cosinus kąta nachylenia najdłuższej krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy jest równy 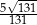 . . | P | F |
Koło ma promień równy 4. Obwód wycinka tego koła o kącie środkowym 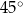 jest równy
jest równy
A) 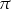 B)
B) 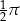 C)
C) 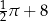 D)
D) 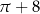
Trójkąty prostokątne 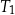 i
i 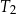 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 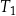 mają długości 7 i 24. Przeciwprostokątna trójkąta
mają długości 7 i 24. Przeciwprostokątna trójkąta 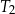 ma długość 50. Oblicz pole trójkąta
ma długość 50. Oblicz pole trójkąta 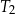 .
.
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich pracowników pewnej firmy za luty 2024 roku.
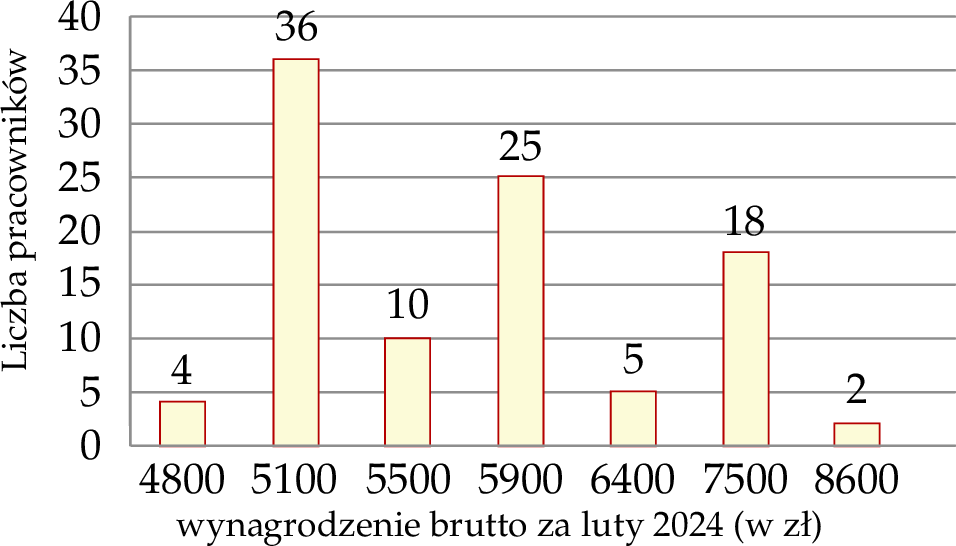
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Zarobki ponad połowy pracowników tej firmy są wyższe od średniej. | P | F |
| Mediana przedstawionych zarobków jest równa 5900 zł. | P | F |
Ze zbioru 99 kolejnych liczb naturalnych – od 1 do 99 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 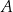 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia 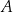 .
.