/Szkoła średnia/Zadania maturalne/Matura 2024/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 20 kwietnia 2024 Czas pracy: 180 minut
Na osi liczbowej zaznaczono sumę przedziałów.

Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A) 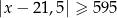 B)
B) 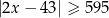
C) 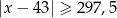 D)
D) 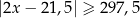
Dla każdej dodatniej liczby rzeczywistej  wyrażenie
wyrażenie 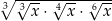 jest równe
jest równe
A) 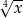 B)
B) 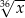 C)
C) 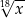 D)
D) 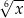
Pan Łukasz wpłacił do banku pewną kwotę na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości 5% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania pan Łukasz odebrał z tego banku wraz z odsetkami kwotę 5292 zł (bez uwzględnienia podatków). Kwota wpłacona przez pana Łukasza na tę lokatę była równa
A) 4800 zł B) 4400 zł C) 4500 zł D) 4600 zł
Liczba 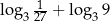 jest równa
jest równa
A) 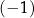 B)
B) 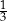 C) 3 D) 10
C) 3 D) 10
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 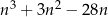 jest podzielna przez 6.
jest podzielna przez 6.
Informacja do zadań 6.1 – 6.4
W kartezjańskim układzie współrzędnych 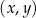 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 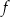 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 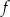 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
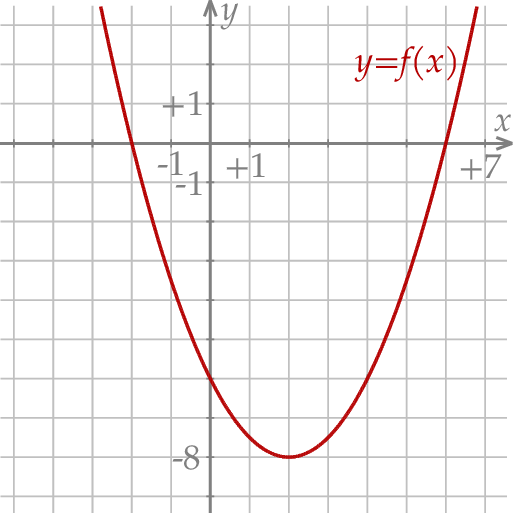
Wyznacz zbiór wszystkich argumentów, dla których funkcja 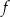 przyjmuje wartości z przedziału
przyjmuje wartości z przedziału ![[− 6,0 ]](https://img.zadania.info/zes/0066695/HzesT21x.png) .
.
Zbiorem wartości funkcji 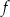 jest przedział
jest przedział
A) ![(− ∞ ,2]](https://img.zadania.info/zes/0066695/HzesT23x.png) B)
B) ![(− ∞ ,− 8]](https://img.zadania.info/zes/0066695/HzesT24x.png) C)
C) 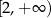 D)
D) 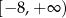
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór funkcji 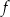 można przedstawić w postaci:
można przedstawić w postaci:
A) 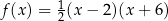 B)
B) 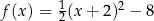
C) 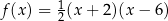 D)
D) 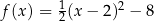
E) 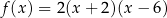 F)
F) 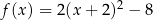
Funkcja kwadratowa 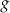 jest określona za pomocą funkcji
jest określona za pomocą funkcji 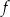 następująco:
następująco: 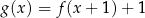 . Fragment wykresu funkcji
. Fragment wykresu funkcji 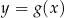 przedstawiono na rysunku
przedstawiono na rysunku
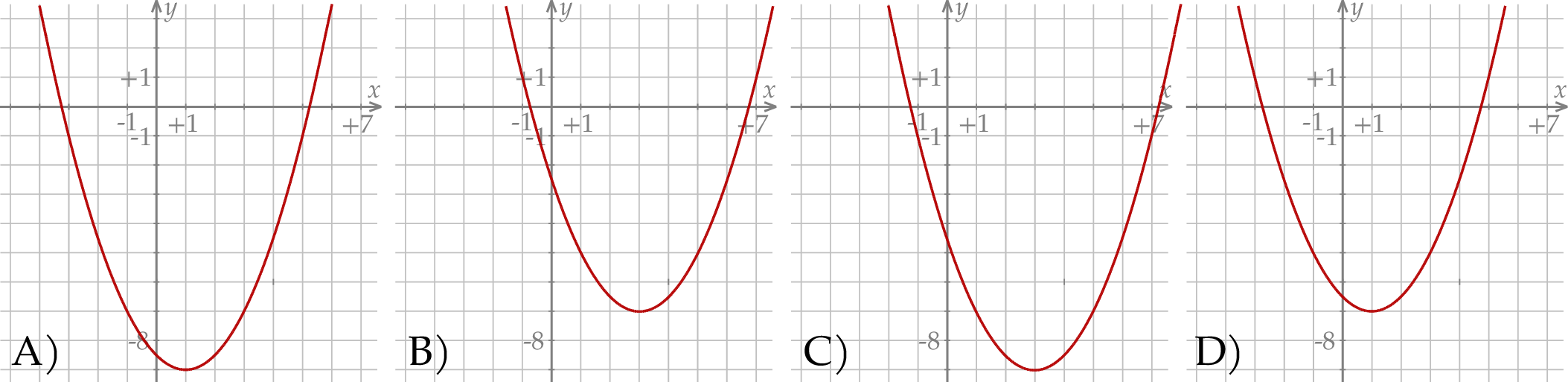
Dla każdej liczby rzeczywistej  różnej od
różnej od 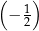 ,
,  , 0 i
, 0 i 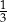 wartość wyrażenia
wartość wyrażenia
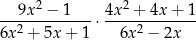
jest równa wartości wyrażenia
A) 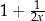 B)
B) 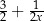 C)
C) 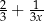 D)
D) 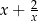
Podstawa 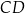 trapezu równoramiennego
trapezu równoramiennego 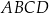 , który nie jest równoległobokiem, ma równanie
, który nie jest równoległobokiem, ma równanie 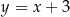 . Ponadto
. Ponadto 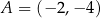 i
i 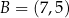 . Oś symetrii tego trapezu ma równanie
. Oś symetrii tego trapezu ma równanie
A) 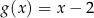 B)
B) 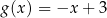 C)
C) 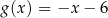 D)
D) 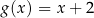
Zbiorem wszystkich rozwiązań nierówności
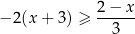
jest przedział
A) ![(− ∞ ,− 4]](https://img.zadania.info/zes/0066695/HzesT58x.png) B)
B) ![(− ∞ ,4]](https://img.zadania.info/zes/0066695/HzesT59x.png) C)
C) 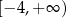 D)
D) 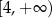
Rozwiąż równanie 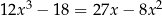 .
.
Funkcja liniowa 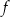 jest określona wzorem
jest określona wzorem 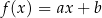 , gdzie
, gdzie  i
i 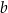 są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji
są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji 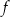 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 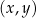 .
.
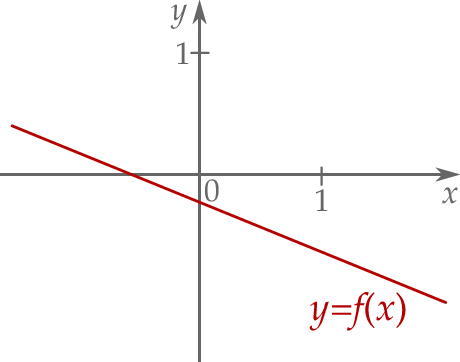
Liczba  oraz liczba
oraz liczba 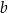 we wzorze funkcji
we wzorze funkcji 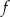 spełniają warunki:
spełniają warunki:
A) 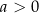 i
i 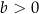 B)
B) 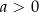 i
i 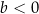 C)
C) 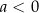 i
i 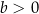 D)
D) 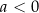 i
i 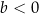
Pięciowyrazowy ciąg 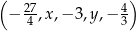 jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
A) 81 B) 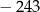 C)
C) 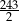 D)
D) 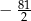
Równanie
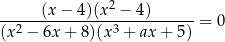
z niewiadomą  nie ma rozwiązań rzeczywistych. Liczba
nie ma rozwiązań rzeczywistych. Liczba  jest więc równa
jest więc równa
A) 6,5 B) 4 C) 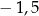 D)
D) 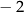
Objętość ostrosłupa prawidłowego trójkątnego jest równa 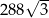 . Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 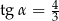 .
.
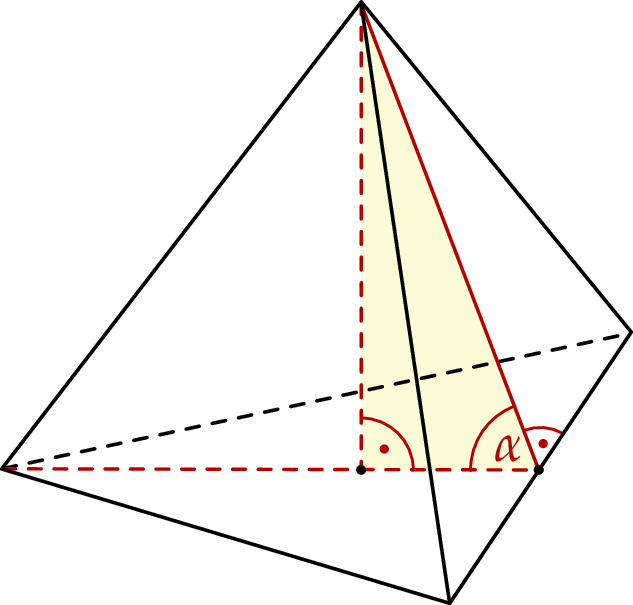
Oblicz wysokość ściany bocznej tego ostrosłupa.
Informacja do zadań 15.1 – 15.3
W kartezjańskim układzie współrzędnych 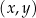 narysowano wykres funkcji
narysowano wykres funkcji 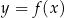 (zobacz rysunek).
(zobacz rysunek).
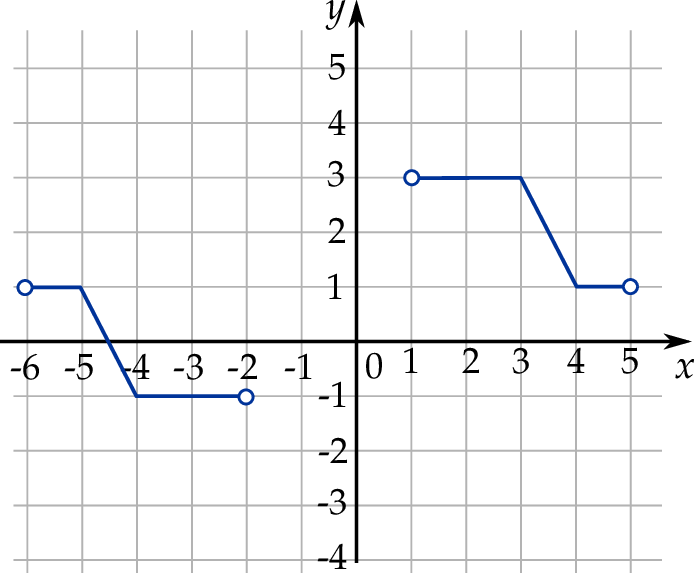
Zapisz poniżej zbiór wszystkich rozwiązań nierówności 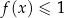 .
.
Dziedziną funkcji 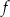 jest zbiór
jest zbiór
A) ![[− 1,1)∪ (1 ,3]](https://img.zadania.info/zes/0066695/HzesT99x.png) B)
B) ![[− 1,3]](https://img.zadania.info/zes/0066695/HzesT100x.png) C)
C) 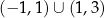
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zes/0066695/HzesT102x.png) E)
E) 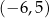 F)
F) 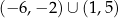
Zbiorem wartości funkcji 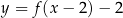 jest zbiór
jest zbiór
A) ![[− 3,1]](https://img.zadania.info/zes/0066695/HzesT106x.png) B)
B) ![[− 1 ,3 ]](https://img.zadania.info/zes/0066695/HzesT107x.png) C)
C) 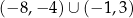
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zes/0066695/HzesT109x.png) E)
E) ![[1,5]](https://img.zadania.info/zes/0066695/HzesT110x.png) F)
F) ![[− 5,− 3]](https://img.zadania.info/zes/0066695/HzesT111x.png)
Pan Tomasz spłacił pożyczkę w wysokości 26760 zł w 24 ratach. Pierwsze 13 rat miało tą samą wysokość, a każda kolejna rata była o 60 zł mniejsza od poprzedniej. Oblicz kwotę pierwszej raty.
Dane są proste 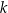 i
i 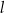 o równaniach
o równaniach
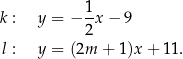
Proste 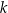 oraz
oraz 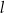 są równoległe, gdy
są równoległe, gdy
A) 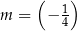 B)
B) 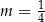 C)
C) 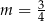 D)
D) 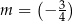
Dla każdego kąta ostrego  wyrażenie
wyrażenie 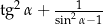 jest równe
jest równe
A) 1 B)  C)
C) 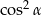 D)
D) 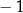
W rombie 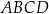 o polu
o polu 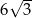 dłuższa przekątna
dłuższa przekątna 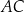 tworzy z bokiem
tworzy z bokiem 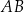 kąt o mierze
kąt o mierze 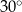 (zobacz rysunek).
(zobacz rysunek).
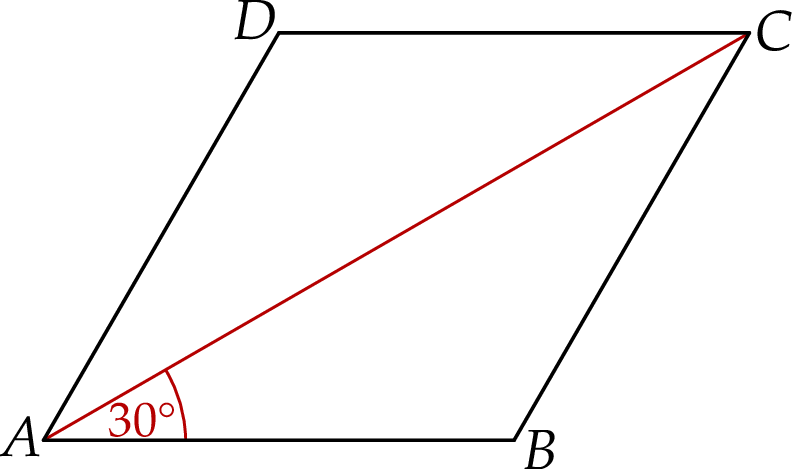
Długość przekątnej 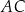 jest równa
jest równa
A) 6 B) 9 C) 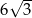 D)
D) 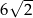
Punkty 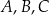 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 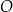 . Kąt
. Kąt 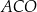 ma miarę
ma miarę 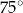 (zobacz rysunek).
(zobacz rysunek).
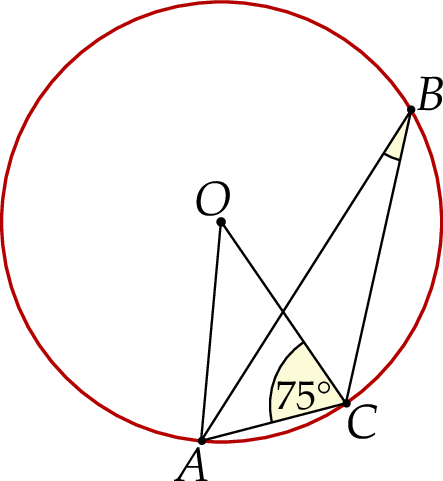
Miara kąta ostrego 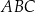 jest równa
jest równa
A) 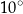 B)
B) 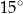 C)
C) 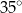 D)
D) 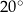
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna ściany bocznej graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 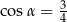 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 25 B) 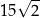 C)
C) 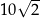 D) 20
D) 20
W kartezjańskim układzie współrzędnych 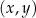 , punkt
, punkt 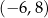 jest punktem przecięcia prostych o równaniach
jest punktem przecięcia prostych o równaniach
A) 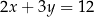 i
i 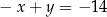 B)
B) 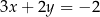 i
i 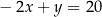
C) 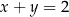 i
i 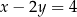 D)
D) 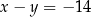 i
i 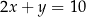
Pole trójkąta równobocznego 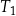 jest równe
jest równe 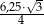 . Pole trójkąta równobocznego
. Pole trójkąta równobocznego 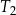 jest równe
jest równe 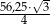 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Trójkąt 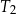 jest podobny do trójkąta
jest podobny do trójkąta 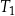 w skali
w skali
| A) 5, | B) 3, |
ponieważ
| 1) | pole trójkąta 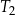 jest 25 razy większe od pola trójkąta jest 25 razy większe od pola trójkąta 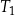 . . |
| 2) | bok trójkąta 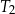 jest o 5 dłuższy od boku trójkąta jest o 5 dłuższy od boku trójkąta 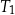 . . |
| 3) | bok trójkąta 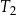 jest 3 razy dłuższy od boku trójkąta jest 3 razy dłuższy od boku trójkąta 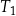 . . |
Informacja do zadań 24.1 i 24.2
Na diagramie poniżej przedstawiono ceny ogórków w szesnastu wybranych sklepach.
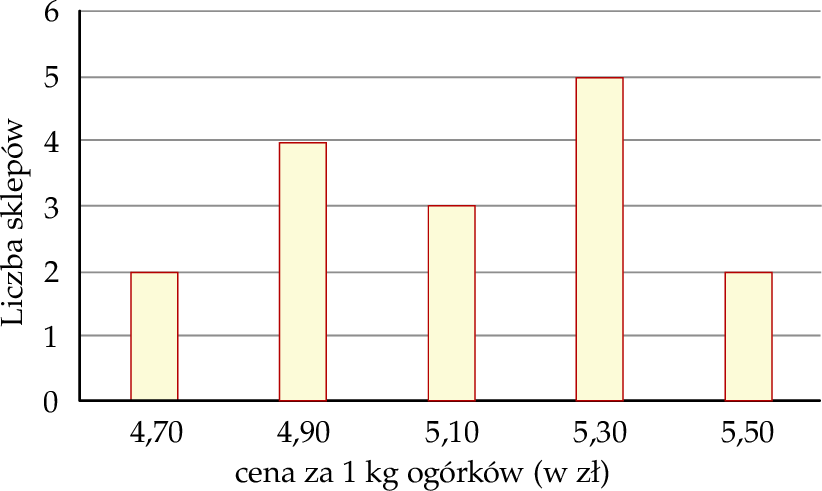
Mediana ceny kilograma ogórków w tych wybranych sklepach jest równa
A) 4,80 zł B) 4,90 zł C) 5,00 zł D) 5,10 zł E) 5,20 zł
Średnia cena kilograma ogórków w tych wybranych sklepach, zaokrąglona do dwóch miejsc po przecinku, jest równa
A) 5,10 zł B) 5,14 zł C) 5,11 zł D) 5,13 zł E) 5,12 zł
W kartezjańskim układzie współrzędnych 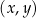 punkty
punkty 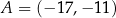 i
i 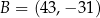 są wierzchołkami równoległoboku
są wierzchołkami równoległoboku 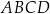 . Punkt
. Punkt 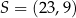 jest środkiem symetrii tego równoległoboku. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest środkiem symetrii tego równoległoboku. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Równoległobok 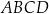 jest rombem. jest rombem. | P | F |
Równoległobok 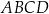 jest prostokątem. jest prostokątem. | P | F |
E–dowód ma zapisany na pierwszej stronie specjalny sześciocyfrowy numer CAN, który zabezpiecza go przed odczytaniem danych przez osoby nieuprawnione. Oblicz, ile jest wszystkich sześciocyfrowych numerów CAN o różnych cyfrach, spełniających warunek: trzy pierwsze cyfry są kolejnymi wyrazami ciągu arytmetycznego o różnicy mniejszej niż 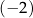 .
.
Ze zbioru liczb 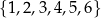 losujemy dwa razy po jednej liczbie ze zwracaniem. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
losujemy dwa razy po jednej liczbie ze zwracaniem. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania dwóch liczb, których suma dzieli się przez 9 jest większe od 0,1. | P | F |
| Prawdopodobieństwo tego, że pierwsza liczba dzieli drugą jest mniejsze niż 0,38. | P | F |
Ciąg 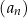 jest określony wzorem
jest określony wzorem 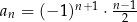 dla każdej liczby naturalnej
dla każdej liczby naturalnej 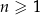 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 2 B) 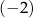 C) 3 D)
C) 3 D) 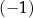
Działka ma kształt trójkąta o podstawie 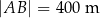 . Wysokość trójkąta opuszczona na podstawę
. Wysokość trójkąta opuszczona na podstawę 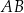 jest równa 125 m, a jego kąty
jest równa 125 m, a jego kąty 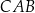 i
i 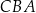 są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie
są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie 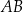 tego trójkąta, a dwa pozostałe –
tego trójkąta, a dwa pozostałe – 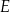 oraz
oraz 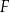 – na bokach
– na bokach 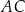 i
i  trójkąta (zobacz rysunek).
trójkąta (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.

