/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2024
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 13 kwietnia 2024 Czas pracy: 100 minut
Poniżej przedstawiono listę produktów, z których przygotowano 8 identycznych paczek świątecznych.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Do przygotowania kolejnych 17 paczek świątecznych, o takiej samej zawartości jak pierwsze 8 paczek, potrzeba ponad 6 kg suszonych owoców. | P | F |
| Gdyby przygotować 73 paczki świąteczne, o takiej samej zawartości jak 8 paczek opisanych w treści zadania, to w tych 73 paczkach liczba pierniczków byłaby równa sumie liczby mandarynek i liczby lizaków. | P | F |
Paulina jest dwa razy starsza od swojego brata Tomka, który z kolei jest osiem razy młodszy od ich mamy. Tomek, Paulina i ich mama mają razem 44 lata. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Za 3 lata Tomek będzie młodszy od Pauliny o A/B
A) 7 lat. B) 4 lata.
Paulina za C/D będzie trzy razy młodsza od mamy.
C) 4 lata D) 6 lat
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje wartość 0 dla 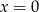 oraz dla
oraz dla 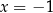 . Które to wyrażenie?
. Które to wyrażenie?
A) 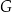 B)
B) 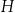 C)
C) 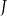 D)
D) 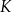
Rozwiązaniem równania 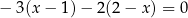 jest liczba
jest liczba
A)  B)
B) 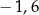 C)
C) 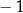 D) 4 E) 8
D) 4 E) 8
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wyrażenie 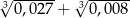 jest równe A/B .
jest równe A/B .
A) 0,5 B) 0,25
Wyrażenie 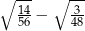 jest równe C/D .
jest równe C/D .
C) 0,25 D) 0,5
O godzinie 10:50 Magda wyruszyła w podróż pociągiem z Krakowa do Żywca. Najpierw dojechała do Katowic, gdzie miała przesiadkę na pociąg do Żywca. Do Źywca dojechała o godzinie 13:35. Na rysunku pokazano, jak w czasie przebiegała podróż Magdy. Na osi czas przejazdu z Krakowa do Żywca podzielono na jednakowe odstępy.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Magda dojechała do Katowic o godzinie 11:35. | P | F |
| Czas oczekiwania na pociąg w Katowicach stanowił mniej niż 20% całego czasu podróży. | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Iloraz 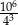 jest równy A/B .
jest równy A/B .
A) 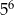 B)
B) 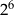
Iloczyn 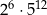 jest równy C/D .
jest równy C/D .
C) 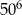 D)
D) 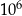
Na tablicy zapisano wszystkie różne liczby dwucyfrowe, które jednocześnie spełniają trzy warunki: są większe od 60, są podzielne przez 3, suma cyfr każdej z nich jest większa od 12. Ile liczb zapisano na tablicy?
A) 3 B) 4 C) 5 D) 6
Pewien ostrosłup ma o 113 więcej krawędzi, niż wierzchołków. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Graniastosłup o takiej samej podstawie, jaką ma ten ostrosłup, ma A/B ścian.
A) 114 B) 116
Wielokąt w podstawie ostrosłupa ma o C/D więcej krawędzi, niż jego jedna ściana boczna.
C) 111 D) 112
Cenę laptopa obniżono najpierw o 200 zł, a następnie cenę obniżono o 30%. Po tych dwóch obniżkach pani Kasia kupiła tego laptopa za 1750 zł. Jaka była cena laptopa przed obniżkami?
A) 2500 zł. B) 2400 zł. C) 2700 zł. D) 2785 zł.
Z urny, w której jest wyłącznie 16 kul białych i 24 kule czarne, losujemy 1 kulę.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wylosowania kuli białej jest równe 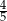 . . | P | F |
Prawdopodobieństwo wylosowania kuli czarnej jest większe od  | P | F |
Dany jest wzór na pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego:
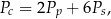
gdzie: 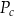 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 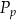 – pole podstawy,
– pole podstawy, 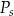 – pole powierzchni jednej ściany bocznej. Pole ściany bocznej
– pole powierzchni jednej ściany bocznej. Pole ściany bocznej 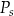 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 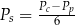 B)
B) 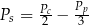 C)
C) 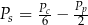 D)
D) 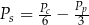
Piotrek na dużej kartce w kratkę narysował figurę złożoną z 60 połączonych odcinków, które kolejno ponumerował liczbami naturalnymi od 1 do 60. Wszystkie komórki kratki są takimi samymi kwadratami. Na rysunku przedstawiono fragment tej figury, złożony z 17 początkowych odcinków. Kolejne odcinki tej figury Piotrek narysował według tej samej reguły, którą zastosował do narysowania odcinków 1–17.
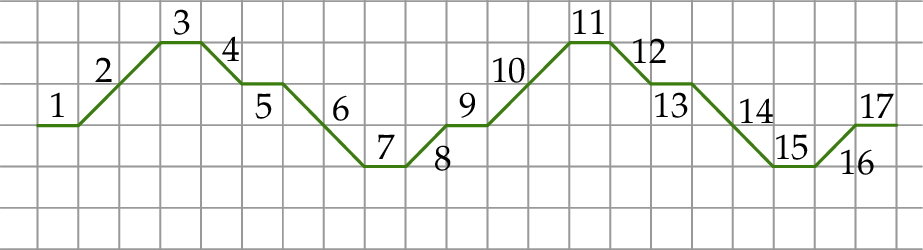
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Proste zawierające odcinki o numerach 39 oraz 53 są wzajemnie równoległe. | P | F |
| Proste zawierające odcinki o numerach 27 oraz 49 są wzajemnie prostopadłe. | P | F |
Na rysunku przedstawiono trójkąt i dwa prostokąty  i
i  oraz podano długości ich boków.
oraz podano długości ich boków.
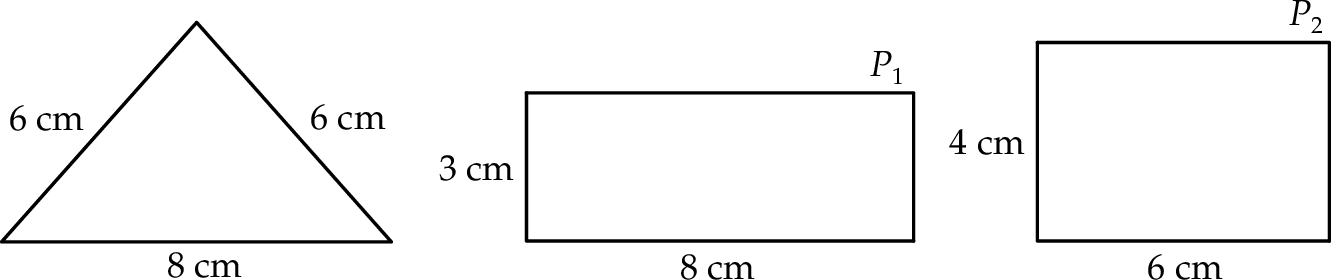
Czy te trzy wielokąty mogą być ścianami jednego graniastosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | każdy z prostokątów 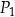 i i 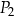 ma bok takiej samej długości jak jeden z boków trójkąta. ma bok takiej samej długości jak jeden z boków trójkąta. |
| B) | prostokąty 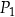 i i 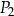 nie mają takich samych wymiarów. nie mają takich samych wymiarów. |
| C) | prostokąty 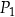 i i 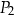 nie mają boku tej samej długości. nie mają boku tej samej długości. |
W czworokącie 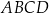 boki
boki 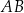 ,
, 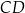 i
i 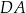 mają równe długości, a kąt
mają równe długości, a kąt 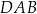 ma miarę
ma miarę 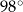 . Przekątna
. Przekątna 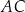 dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt  ma miarę ma miarę  . . | P | F |
Kąt 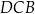 ma miarę ma miarę 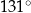 . . | P | F |
Z miejscowości Ząbki do miejscowości Bródka wyruszyły dwa samochody – pierwszym jechał pan Bogdan, drugim pan Wojciech. Każdy z tych dwóch samochodów pokonał całą trasę w tym samym czasie, przy czym pan Wojciech jechał cały czas ze stałą prędkością, a pan Bogdan pierwsze 25 km trasy pokonał w czasie 18 minut, kolejne 20 km pokonał w czasie 16 minut, a pozostałe 35 km trasy pokonał w pół godziny. Oblicz z jaką średnią prędkością samochód pana Wojciecha pokonał trasę między Ząbkami a Bródką. Wynik podaj w kilometrach na godzinę.
Łąka ma kształt równoległoboku i jest podzielona na dwie części 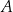 i
i 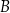 , tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
, tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
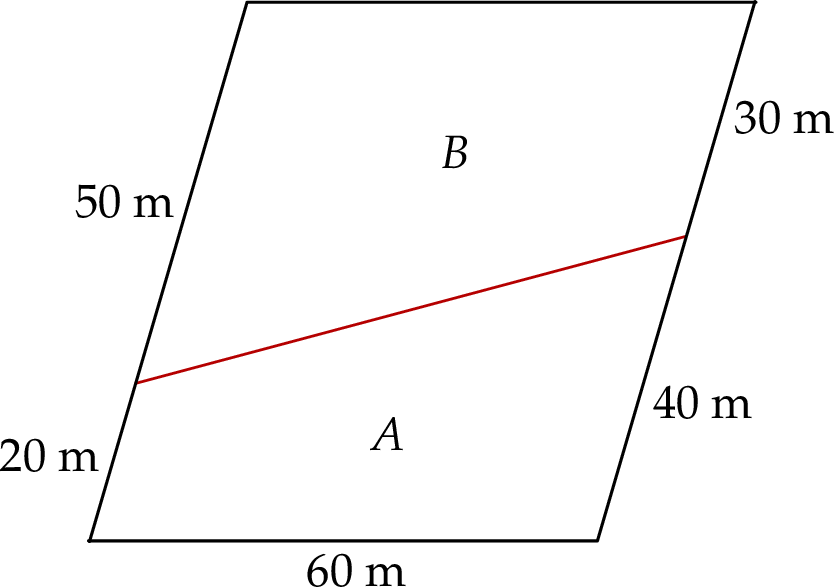
Kosiarka w ciągu każdej godziny swojej pracy kosi trawę z powierzchni o takim samym polu. Kosiarka całą łąkę skosiła w ciągu 14 godzin. Oblicz, ile godzin potrzebowałaby ta kosiarka na skoszenie trawy z części  jest łąki.
jest łąki.
W kasie są banknoty 20–złotowe i 50–złotowe. Liczba banknotów 20–złotowych jest dwa razy większa od liczby banknotów 50–złotowych. Łączna wartość wszystkich banknotów 50–złotowych jest o 3 tysiące złotych większa od łącznej wartości wszystkich banknotów 20–złotowych. Oblicz, ile banknotów 20–złotowych jest w kasie.
Z pięciu prostopadłościennych klocków o jednakowych wymiarach ułożono figurę. Kształt i wybrane wymiary tej figury przedstawiono na rysunku.
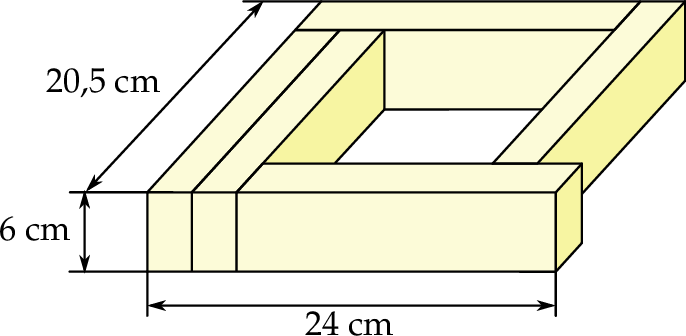
Oblicz objętość jednego klocka.

